【题目】某校有
、
、
、
四件作品参加航模类作品比赛.已知这四件作品中恰有两件获奖，在结果揭晓前，甲、乙、丙、丁四位同学对这四件参赛作品的获奖情况预测如下.
甲说：“、同时获奖.”
乙说：“、不可能同时获奖.”
丙说：“获奖.”
丁说：“、至少一件获奖”
如果以上四位同学中有且只有两位同学的预测是正确的，则获奖的作品是（ ）
A. 作品与作品B. 作品与作品C. 作品与作品D. 作品与作品
科目：高中数学 来源： 题型：
【题目】从甲、乙两名学生中选拔一人参加射箭比赛，为此需要对他们的射箭水平进行测试．现这两名学生在相同条件下各射箭10次，命中的环数如下：
甲 | 8 | 9 | 7 | 9 | 7 | 6 | 10 | 10 | 8 | 6 |
乙 | 10 | 9 | 8 | 6 | 8 | 7 | 9 | 7 | 8 | 8 |
(1)计算甲、乙两人射箭命中环数的平均数和标准差；
(2)比较两个人的成绩，然后决定选择哪名学生参加射箭比赛．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知向量
（1）若
分别表示将一枚质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次时第一次，第二次出现的点数，求满足
的概率；
（2）若在连续区间[1,6]上取值，求满足
的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某班同学利用国庆节进行社会实践，对
岁的人群随机抽取
人进行了一次生活习惯是否符合低碳观念的调查，若生活习惯符合低碳观念的称为“低碳族”，否则称为“非低碳族”，得到如下统计表和各年龄段人数频率分布直方图：
组数 | 分组 | 低碳族的人数 | 占本组的频率 |
第一组 |
| 120 | 0.6 |
第二组 |
| 195 |
|
第三组 |
| 100 | 0.5 |
第四组 |
|
| 0.4 |
第五组 |
| 30 | 0.3 |
第六组 |
| 15 | 0.3 |
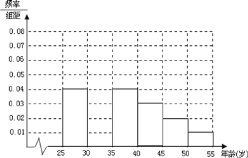
（1）补全频率分布直方图并求、
、
的值；
（2）从
岁年龄段的“低碳族”中采用分层抽样法抽取18人参加户外低碳体验活动，如何抽取？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
的部分图象如图所示，且相邻的两个最值点的距离为
.
（1）求函数
的解析式；
（2）若将函数的图象向左平移1个单位长度后得到函数
的图象，关于
的不等式
在
上有解，求
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知集合P＝{x|a＋1≤x≤2a＋1}，Q＝{x|x2－3x≤10}．
(1)若a＝3，求(RP)∩Q；
(2)若P∪Q＝Q，求实数a的取值范围．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
