
【题目】如图,在![]() 中,已知
中,已知![]() ,
,![]() 在
在![]() 上,且
上,且![]() ,又
,又![]() 平面
平面![]() .
.
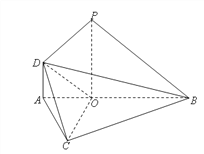
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
【答案】(Ⅰ)见解析;(Ⅱ)![]() .
.
【解析】分析:(Ⅰ)设OA=1,则PO=OB=2,DA=1,由DA∥PO,PO⊥平面ABC,知DA⊥平面ABC,可得DA⊥AO.利用勾股定理的逆定理可得:PD⊥DO.由OC=OB=2,∠ABC=45°,可得CO⊥AB,又PO⊥平面ABC,可得PO⊥OC,得到CO⊥平面PAB.得到CO⊥PD.即可证明.
(Ⅱ)如图建立空间直角坐标系,点A为坐标原点,设AB=1,利用线面垂直的性质、向量垂直与数量积的关系得出两个平面的法向量,求出其夹角即可.
详解:(Ⅰ)证明:设OA=1,则PO=OB=2,DA=1,
由DA∥PO,PO⊥平面ABC,知DA⊥平面ABC,
∴DA⊥AO.从而![]() ,
,
在△PDO中,∵PO=2,
∴△PDO为直角三角形,故PD⊥DO.
又∵OC=OB=2,∠ABC=45°,
∴CO⊥AB,又PO⊥平面ABC,
∴PO⊥OC,
又PO,AB平面PAB,PO∩AB=O,
∴CO⊥平面PAB.
故CO⊥PD.
∵CO∩DO=O,
∴PD⊥平面COD.
(Ⅱ)解:以OC,OB,OP所在射线分别为x,y,z轴,建立直角坐标系如图.
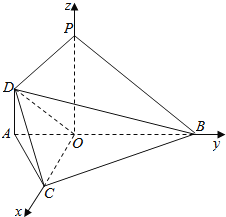
则由(Ⅰ)知,C(2,0,0),B(0,2,0),P(0,0,2),D(0,﹣1,1),
∴![]() ,
,
由(Ⅰ)知PD⊥平面COD,∴![]() 是平面DCO的一个法向量,
是平面DCO的一个法向量,
设平面BDC的法向量为![]() ,∴
,∴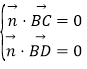 ,∴
,∴![]() ,
,
令y=1,则x=1,z=3,∴![]() ,
,
∴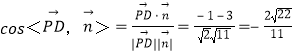 ,
,
由图可知:二面角B﹣DC﹣O为锐角,二面角B﹣DC﹣O的余弦值为![]() .
.


 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga(x+1)﹣loga(1﹣x),a>0且a≠1.
(1)求f(x)的定义域;
(2)判断f(x)的奇偶性并予以证明;
(3)当a>1时,求使f(x)>0的x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an}中,已知a1=2,an+1=3an+2n﹣1.
(1)求证:数列{an+n}为等比数列;
(2)记bn=an+(1﹣λ)n,且数列{bn}的前n项和为Tn , 若T3为数列{Tn}中的最小项,求λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=3sinx﹣πx,命题p:x∈(0, ![]() ),f(x)<0,则( )
),f(x)<0,则( )
A.p是假命题,¬p:?x∈(0, ![]() ),f(x)≥0
),f(x)≥0
B.p是假命题,¬p:?x0∈(0, ![]() ),f(x0)≥0
),f(x0)≥0
C.p是真命题,¬p:?x∈(0, ![]() ),f(x)>0
),f(x)>0
D.p是真命题,¬p:?x0∈(0, ![]() ),f(x0)≥0
),f(x0)≥0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校举办的集体活动中,设计了如下有奖闯关游戏:参赛选手按第一关、第二关、第三关的顺序依次闯关,若闯关成功,分别获得1分、2分、3分的奖励,游戏还规定,当选手闯过一关后,可以选择得到相应的分数,结束游戏;也可以选择继续闯下一关,若有任何一关没有闯关成功,则全部分数都归零,游戏结束。设选手甲第一关、第二关、第三关的概率分别为![]() ,
,![]() ,
,![]() ,选手选择继续闯关的概率均为
,选手选择继续闯关的概率均为![]() ,且各关之间闯关成功互不影响
,且各关之间闯关成功互不影响
(I)求选手甲第一关闯关成功且所得分数为零的概率
(II)设该学生所得总分数为X,求X的分布列与数学期望
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面五边形![]() 是轴对称图形(如图1),BC为对称轴,AD⊥CD,AD=AB=1,
是轴对称图形(如图1),BC为对称轴,AD⊥CD,AD=AB=1,![]() ,将此五边形沿BC折叠,使平面ABCD⊥平面BCEF,得到如图2所示的空间图形,对此空间图形解答下列问题.
,将此五边形沿BC折叠,使平面ABCD⊥平面BCEF,得到如图2所示的空间图形,对此空间图形解答下列问题.


(1)证明:AF∥平面DEC;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】南航集团与波音公司2018年2月在广州签署协议,双方合作的客改货项目落户广州空港经济区.根据协议,双方将在维修技术转让、支持项目、管理培训等方面开展战略合作.现组织者对招募的100名服务志愿者培训后,组织一次知识竞赛,将所得成绩制成如下频率分布直方图(假定每个分数段内的成绩均匀分布),组织者计划对成绩前20名的参赛者进行奖励.

(1)试求受奖励的分数线;
(2)从受奖励的20人中利用分层抽样抽取5人,再从抽取的5人中抽取2人在主会场服务,试求2人成绩都在90分以上(含90分)的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4﹣4:坐标系与参数方程 曲线C1的参数方程为 ![]() (α为参数),在以原点O为极点,x轴的正半轴为极轴的极坐标系中,曲线C2的极坐标方程为ρcos2θ=sinθ.
(α为参数),在以原点O为极点,x轴的正半轴为极轴的极坐标系中,曲线C2的极坐标方程为ρcos2θ=sinθ.
(1)求曲线C1的极坐标方程和曲线C2的直角坐标方程;
(2)若射线l:y=kx(x≥0)与曲线C1 , C2的交点分别为A,B(A,B异于原点),当斜率k∈(1, ![]() ]时,求|OA||OB|的取值范围.
]时,求|OA||OB|的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com