
 某市对所有高校学生进行普通话水平测试,发现成绩服从正态分布N(μ,σ2),下表用茎叶图列举出来抽样出的10名学生的成绩.
某市对所有高校学生进行普通话水平测试,发现成绩服从正态分布N(μ,σ2),下表用茎叶图列举出来抽样出的10名学生的成绩.分析 (1)利用公式,计算这10名学生的成绩的均值和方差;
(2)由(1)可估计,μ=90,σ=7.利用P(76<x<97)=P(μ-2σ<x<μ)+P(μ<x<μ+σ),可得结论.
解答 解:(1)$\overline{x}$=90,S2=$\frac{1}{10}×(1{1}^{2}+1{0}^{2}+{5}^{2}+{5}^{2}+0+{3}^{2}+{5}^{2}+{6}^{2}+{7}^{2}+1{0}^{2})$=49.…(6分)
(2)由(1)可估计,μ=90,σ=7.
P(76<x<97)=P(μ-2σ<x<μ)+P(μ<x<μ+σ)=$\frac{0.9544}{2}$+$\frac{0.6826}{2}$=0.8185.…(12分)
点评 本题考查茎叶图,考查正态分布,考查学生的计算能力,比较基础.


 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
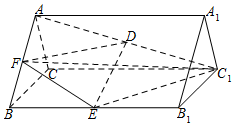 如图,在正三棱柱ABC-A1B1C1中,AB=2,AA1=3,D,E分别为AC1和BB1的中点.
如图,在正三棱柱ABC-A1B1C1中,AB=2,AA1=3,D,E分别为AC1和BB1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 9 | D. | -9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知抛物线E:y2=2px(P>0)的准线为x=-1,M,N为直线x=-2上的两点,M,N两点的纵坐标之积为-8,P为抛物线上一动点,PN,PM,分别交抛物线于A,B两点.
已知抛物线E:y2=2px(P>0)的准线为x=-1,M,N为直线x=-2上的两点,M,N两点的纵坐标之积为-8,P为抛物线上一动点,PN,PM,分别交抛物线于A,B两点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | b<a<c | C. | c<a<b | D. | a<c<b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com