
 =(
=( sin
sin ,1),
,1), =(cos
=(cos ,cos2
,cos2 ).记f(x)=
).记f(x)=

 sin
sin cos
cos +cos2
+cos2
 sin
sin +
+
 cos
cos
 +
+ )
) .
.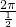 =4π.
=4π. ≤
≤ +
+ ≤2kπ+
≤2kπ+ ,(k∈Z).
,(k∈Z).  ≤x≤4kπ+
≤x≤4kπ+ ,
, ,4kπ+
,4kπ+ ](k∈Z).
](k∈Z). +
+ ∈(
∈( ),
), <sin(
<sin( +
+ )≤1,
)≤1, ].
]. =(
=( sin
sin ,1),
,1), =(cos
=(cos ,cos2
,cos2 ).f(x)=
).f(x)= 根据平面向量的数量积公式,结合降幂公式(二倍角公式逆用)及辅助角公式,将函数的解析式化为正弦型函数的形式,进而根据正弦型函数的性质,即可求出函数的周期,求出函数f(x)的单调递增区间;
根据平面向量的数量积公式,结合降幂公式(二倍角公式逆用)及辅助角公式,将函数的解析式化为正弦型函数的形式,进而根据正弦型函数的性质,即可求出函数的周期,求出函数f(x)的单调递增区间;

 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:高中数学 来源: 题型:
| a |
| b |
| 3 |
| a |
| b |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 19 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| a |
| b |
| a |
| b |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| 3 |
| a |
| b |
| π |
| 2 |
| 3 |
| 5 |
| π |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com