
分析 (Ⅰ)先求函数f(x)的导函数,函数f(x)的图象上有与x轴平行的切线,即导函数为零时有实数解,再令方程的判别式大于或等于零即可得a的范围
(Ⅱ)先由f′(-1)=0求出a值;从而求出求函数f(x)在[-1,0]上的最大值和最小值,当这两个值差的绝对值小于$\frac{5}{16}$,即证明了x1、x2∈(-1,0)时,不等式|f(x1)-f(x2)|<$\frac{5}{16}$恒成立.
解答 解:∵f(x)=x3+ax2+$\frac{3}{2}$x+$\frac{3}{2}$a,∴f′(x)=3x2+2ax+$\frac{3}{2}$,
(Ⅰ)∵函数f(x)的图象有与x轴平行的切线,
∴f′(x)=0有实数解则△=4a2-4×3×$\frac{3}{2}$≥0,a2≥$\frac{9}{2}$,
所以a的取值范围是(-∞,-$\frac{3\sqrt{2}}{2}$]∪[$\frac{3\sqrt{2}}{2}$,+∞)
(Ⅱ)证明:∵f′(-1)=0,∴3-2a+$\frac{3}{2}$=0,a=$\frac{9}{4}$,
∴f′(x)=3x2+$\frac{9}{2}$x+$\frac{3}{2}$=3(x+$\frac{1}{2}$)(x+1)
由f'(x)>0得x<-1或x>-$\frac{1}{2}$;
由f′(x)<0得-1<x<-$\frac{1}{2}$,
∴f(x)的单调递增区间是(-∞,-1),(-$\frac{1}{2}$,+∞),单调减区间为(-1,-$\frac{1}{2}$);
∴f(x)的最大值为f(-1)=$\frac{25}{8}$,
f(x)的极小值为f(-$\frac{1}{2}$)=$\frac{49}{16}$,又f(0)=$\frac{27}{8}$,
∴f(x)在[-1,0]上的最大值M=$\frac{27}{8}$,最小值m=$\frac{49}{16}$,
∴对任意x1,x2∈(-1,0),
恒有|f(x1)-f(x2)|<M-m=$\frac{5}{16}$.
点评 本题综合考查了导数在研究函数性质中的应用,特别是在研究函数单调性和最值上的应用,解题时要透彻理解导数的几何意义,规范在求单调区间及最值时的解题步骤.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
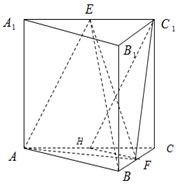 如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB=AC,E,F,H分别是A1C1,BC,AC的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB=AC,E,F,H分别是A1C1,BC,AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a>b,则ac2>bc2 | B. | 若a>b>0,c>d>0,则$\frac{a}{d}>\frac{b}{c}$ | ||
| C. | 若a<b<0,则ab<b2 | D. | 若$\frac{a}{b}>1$,则a>b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | 1 | C. | $\frac{5}{4}$ | D. | $\frac{7}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | b>a>c | B. | c>b>a | C. | c>a>b | D. | a>c>b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com