
(1)如果函数y=x+![]() 在(0,4]上是减函数,在[4,+∞)上是增函数,求实常数b的值;
在(0,4]上是减函数,在[4,+∞)上是增函数,求实常数b的值;
(2)设常数c∈[1,4],求函数f(x)=x+![]() (1≤x≤2)的最大值和最小值;
(1≤x≤2)的最大值和最小值;
(3)当n是正整数时,研究函数g(x)=xn-![]() (c>0)的单调性,并说明理由.
(c>0)的单调性,并说明理由.
解(1) 由已知得![]() =4, ∴b=4.
=4, ∴b=4.
(2) ∵c∈[1,4], ∴![]() ∈[1,2],
∈[1,2],
于是,当x=![]() 时, 函数f(x)=x+
时, 函数f(x)=x+![]() 取得最小值2
取得最小值2![]() .
.
f(1)-f(2)=![]() ,
,
当1≤c≤2时, 函数f(x)的最大值是f(2)=2+![]() ;
;
当2≤c≤4时, 函数f(x)的最大值是f(1)=1+c.
(3)设0<x1<x2,g(x2)-g(x1)=![]() .
.
当![]() <x1<x2时, g(x2)>g(x1), 函数g(x)在[
<x1<x2时, g(x2)>g(x1), 函数g(x)在[![]() ,+∞)上是增函数;
,+∞)上是增函数;
当0<x1<x2<![]() 时, g(x2)>g(x1), 函数g(x)在(0,
时, g(x2)>g(x1), 函数g(x)在(0, ![]() ]上是减函数.
]上是减函数.
当n是奇数时,g(x)是奇函数,
函数g(x) 在(-∞,-![]() ]上是增函数, 在[-
]上是增函数, 在[-![]() ,0)上是减函数.
,0)上是减函数.
当n是偶数时, g(x)是偶函数,
函数g(x)在(-∞,-![]() ]上是减函数, 在[-
]上是减函数, 在[-![]() ,0)上是增函数.
,0)上是增函数.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:高中数学 来源: 题型:
 (2012•武昌区模拟)已知点P在半径为1的半圆周上沿着A→P→B路径运动,设弧 的长度为x,弓形面积为f(x)(如图所示的阴影部分),则关于函数y=f(x)的有如下结论:
(2012•武昌区模拟)已知点P在半径为1的半圆周上沿着A→P→B路径运动,设弧 的长度为x,弓形面积为f(x)(如图所示的阴影部分),则关于函数y=f(x)的有如下结论:查看答案和解析>>
科目:高中数学 来源:湖北省武汉市武昌区2012届高三5月调研考试数学文科试题 题型:013
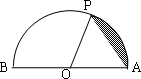
已知点P在半径为1的半圆周上沿着A→P→B路径运动,设弧![]() 的长度为x,弓形面积为f(x)(如图所示的阴影部分),则关于函数y=f(x)的有如下结论:
的长度为x,弓形面积为f(x)(如图所示的阴影部分),则关于函数y=f(x)的有如下结论:
①函数y=f(x)的定义域和值域都是[0,π];
②如果函数y=f(x)的定义域R,则函数y=f(x)是周期函数;
③如果函数y=f(x)的定义域R,则函数y=f(x)是奇函数;
④函数y=f(x)在区间[0,π]上是单调递增函数.
以上结论的正确个数是
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
 已知点P在半径为1的半圆周上沿着A→P→B路径运动,设弧 的长度为x,弓形面积为f(x)(如图所示的阴影部分),则关于函数y=f(x)的有如下结论:
已知点P在半径为1的半圆周上沿着A→P→B路径运动,设弧 的长度为x,弓形面积为f(x)(如图所示的阴影部分),则关于函数y=f(x)的有如下结论:查看答案和解析>>
科目:高中数学 来源:2012年湖北省武汉市武昌区高三五月调考数学试卷(文科)(解析版) 题型:选择题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com