
分析 可设$y=\frac{x}{{x}^{2}+4}$,从而得到yx2+4y=x,进一步可得到yx2-x+4y=0,可看成关于x的方程,方程有解,显然需讨论y:y=0容易判断满足方程有解,而y≠0时,需满足△=1-16y2≥0,这样解出y的范围,并上y=0便可得出原函数的值域.
解答 解:设y=f(x),则:
yx2+4y=x;
∴yx2-x+4y=0,看成关于x的方程,方程有解;
①y=0时,x=0,满足方程有解;
②y≠0时,△=1-16y2≥0;
解得$-\frac{1}{4}≤y≤\frac{1}{4}$;
∴综上得,原函数的值域为$[-\frac{1}{4},\frac{1}{4}]$.
故答案为:[$-\frac{1}{4},\frac{1}{4}$].
点评 考查函数值域的概念,以及形如$y=\frac{a{x}^{2}+bx+c}{d{x}^{2}+ex+f}$的函数值域的求法:整理成关于x的方程的形式,根据方程有解求值域,一元二次方程有解时判别式△的取值情况.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年安徽豪州蒙城县一中高二上月考一数学试卷(解析版) 题型:解答题
已知数列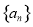 的前
的前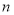 项和
项和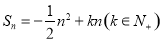 ,且
,且 的最大值为8.
的最大值为8.
(1)确定常数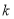 ,并求
,并求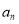 ;
;
(2)求数列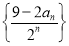 的前
的前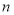 项和
项和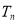 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 空集 | B. | 实数集 | C. | 单元素集 | D. | 二元素集 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{3}$,1) | B. | (-∞,$\frac{1}{3}$)∪(1,+∞) | C. | (-$\frac{1}{3}$,$\frac{1}{3}$) | D. | (-∞,-$\frac{1}{3}$)∪($\frac{1}{3}$,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com