
【题目】已知函数f(x)= ![]()
(1)求证f(x)在(0,+∞)上递增
(2)若f(x)在[m,n]上的值域是[m,n],求实数a的取值范围
(3)当f(x)≤2x在(0,+∞)上恒成立,求实数a的取值范围.
【答案】
(1)证明:∵f(x)= ![]() ﹣
﹣ ![]() ,x∈(0,+∞),
,x∈(0,+∞),
∴f'(x)= ![]() >0,
>0,
故函数f(x)在(0,+∞)上单调递增
(2)∵f(x)在(0,+∞)上单调递增,
∴若f(x)在[m,n]上的值域是[m,n],
则 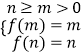 ,即
,即  ,
,
故函数y= ![]() 与y=x+
与y=x+ ![]() (x>0)的图象有两个公共点,
(x>0)的图象有两个公共点,
∵当x>0时,y=x+ ![]() ≥2(当且仅当x=
≥2(当且仅当x= ![]() ,即x=1时取“=”),
,即x=1时取“=”),
∴ ![]() ≥2,解得0<a≤
≥2,解得0<a≤ ![]()
(3)∵f(x)= ![]() ﹣
﹣ ![]() ,f(x)≤2x在(0,+∞)上恒成立上,
,f(x)≤2x在(0,+∞)上恒成立上,
∴a≥ ![]() =
= ![]() 在(0,+∞)上恒成立,
在(0,+∞)上恒成立,
令g(x)= ![]() ,
,
则g(x)≤ ![]() =
= ![]() (当且仅当2x=
(当且仅当2x= ![]() ,即x=
,即x= ![]() 时取等号),
时取等号),
要使(0,+∞)上恒成立,
故a的取值范围是[ ![]() ,+∞)
,+∞)
【解析】(1)利用f'(x)= ![]() >0即可证明f(x)在(0,+∞)上递增;(2)若f(x)在[m,n]上的值域是[m,n],则则
>0即可证明f(x)在(0,+∞)上递增;(2)若f(x)在[m,n]上的值域是[m,n],则则 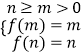 ,构造函数y=
,构造函数y= ![]() 与y=x+
与y=x+ ![]() (x>0),利用两函数的图象有两个公共点,即求实数a的取值范围;(3)当f(x)≤2x在(0,+∞)上恒成立a≥
(x>0),利用两函数的图象有两个公共点,即求实数a的取值范围;(3)当f(x)≤2x在(0,+∞)上恒成立a≥ ![]() =
= ![]() 在(0,+∞)上恒成立,构造函数g(x)=
在(0,+∞)上恒成立,构造函数g(x)= ![]() ,利用基本不等式可求得g(x)max , 从而可求实数a的取值范围.
,利用基本不等式可求得g(x)max , 从而可求实数a的取值范围.
【考点精析】利用函数的值域对题目进行判断即可得到答案,需要熟知求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线y2=4x的焦点为F,过点F的直线交抛物线于A,B两点.
(1)若 ![]() =3
=3 ![]() ,求直线AB的斜率;
,求直线AB的斜率;
(2)设点M在线段AB上运动,原点O关于点M的对称点为C,求四边形OACB面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】山西某公司有一批专业技术人员,对他们进行年龄状况和接受教育程度(本科学历)的调查,其结果(人数分布)如表:
学历 | 35岁以下 | 35 | 50岁以上 |
本科 | 80 | 30 | 20 |
研究生 |
| 20 |
|
(Ⅰ)用分层抽样的方法在![]() 岁年龄段的专业技术人员中抽取一个容量为10的样本,将该样本看成一个总体,从中任取3人,求至少有1人的学历为研究生的概率;
岁年龄段的专业技术人员中抽取一个容量为10的样本,将该样本看成一个总体,从中任取3人,求至少有1人的学历为研究生的概率;
(Ⅱ)在这个公司的专业技术人员中按年龄状况用分层抽样的方法抽取![]() 个人,其中35岁以下48人,50岁以上10人,再从这
个人,其中35岁以下48人,50岁以上10人,再从这![]() 个人中随机抽取出1人,此人的年龄为50岁以上的概率为
个人中随机抽取出1人,此人的年龄为50岁以上的概率为![]() ,求
,求![]() 、
、![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设x取实数,则f(x)与g(x)表示同一个函数的是( )
A.f(x)=x,g(x)= ![]()
B.f(x)= ![]() ,g(x)=
,g(x)= ![]()
C.f(x)=1,g(x)=(x﹣1)0
D.f(x)= ![]() ,g(x)=x﹣3
,g(x)=x﹣3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017北京西城区5月模拟】某大学为调研学生在![]() ,
,![]() 两家餐厅用餐的满意度,从在
两家餐厅用餐的满意度,从在![]() ,
,![]() 两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行评分,满分均为60分.
两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行评分,满分均为60分.
整理评分数据,将分数以10为组距分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到
,得到![]() 餐厅分数的频率分布直方图,和
餐厅分数的频率分布直方图,和![]() 餐厅分数的频数分布表:
餐厅分数的频数分布表:

定义学生对餐厅评价的“满意度指数”如下:
分数 |
|
|
|
满意度指数 |
|
|
|
(Ⅰ)在抽样的100人中,求对![]() 餐厅评价“满意度指数”为0的人数;
餐厅评价“满意度指数”为0的人数;
(Ⅱ)从该校在![]() ,
,![]() 两家餐厅都用过餐的学生中随机抽取1人进行调查,试估计其对
两家餐厅都用过餐的学生中随机抽取1人进行调查,试估计其对![]() 餐厅评价的“满意度指数”比对
餐厅评价的“满意度指数”比对![]() 餐厅评价的“满意度指数”高的概率;
餐厅评价的“满意度指数”高的概率;
(Ⅲ)如果从![]() ,
,![]() 两家餐厅中选择一家用餐,你会选择哪一家?说明理由.
两家餐厅中选择一家用餐,你会选择哪一家?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com