
分析 法1,将正三棱锥A-BCD补充成一个正方体AGBH-FDEC,说明正三棱锥A-BCD和正方体AGBH-FDEC有共同的外接球,设正方体AGBH-FDEC的棱长为a,求推出与正方体外接球半径R的关系,然后求解△BCD的面积.
法2,由条件A-BCD是正四面体,△BCD是正三角形,A,B,C,D为球上四点,球心O在正四面体中心如图5,设BC=a,CD的中点为E,O1为过点B,C,D截面圆圆心,求出截面圆半径,正四面体A-BCD的高.然后求解△BCD的面积.
解答 解:法1,由条件A-BCD是正四面体,△BCD是正三角形,A,B,C,D为球上四点,
将正三棱锥A-BCD补充成一个正方体AGBH-FDEC如图4,
则正三棱锥A-BCD和正方体AGBH-FDEC有共同的外接球,△BCD的边长就是正方体面的对角线,
设正方体AGBH-FDEC的棱长为a,则正方体外接球半径R满足: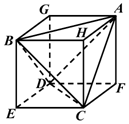
a2+a2+a2=(2R)2,解得${a^2}=\frac{4}{3}{R^2}$,所以BC2=${a^2}+{a^2}=\frac{8}{3}{R^2}$,
△BCD的面积$S=\frac{1}{2}BC×BDsin60°=\frac{1}{2}×\frac{8}{3}{R^2}×\frac{{\sqrt{3}}}{2}=\frac{{2\sqrt{3}}}{3}{R^2}$.
法2,由条件A-BCD是正四面体,△BCD是正三角形,A,B,C,D为球上四点,
球心O在正四面体中心如图5,设BC=a,CD的中点,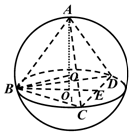
为E,O1为过点B,C,D截面圆圆心,则截面圆半径$r={O_1}B=\frac{2}{3}BE=\frac{2}{3}×\frac{{\sqrt{3}}}{2}a=\frac{{\sqrt{3}}}{3}a$,
正四面体A-BCD的高$A{O_1}=\sqrt{{a^2}-{{(\frac{{\sqrt{3}}}{3}a)}^2}}=\frac{{\sqrt{6}}}{3}a$.
∴截面BCD与球心的距离$d=O{O_1}=\frac{{\sqrt{6}}}{3}a-R$,在Rt△BOO1
中,${(\frac{{\sqrt{3}}}{3}a)^2}={R^2}-{(\frac{{\sqrt{6}}}{3}a-R)^2}$,解得$a=\frac{{2\sqrt{6}}}{3}R$.
∴△BCD的面积为$S=\frac{1}{2}BC×BDsin60°=\frac{1}{2}×{(\frac{{2\sqrt{6}}}{3}R)^2}×\frac{{\sqrt{3}}}{2}=\frac{{2\sqrt{3}}}{3}{R^2}$.
点评 本题考查空间几何体的位置关系的应用,三角形底面积的求法,点线面距离的求法,考查空间想象能力以及计算能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
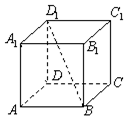 如图,在正方形ABCD-A1B1C1D1中,过对角线BD1的一个平面交AA1于E,交CC1于F,
如图,在正方形ABCD-A1B1C1D1中,过对角线BD1的一个平面交AA1于E,交CC1于F,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 斤 | B. | 9 斤 | C. | 9.5斤 | D. | 12 斤 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\vec a-2\vec b$ | B. | $\overrightarrow{a}$-4$\vec b$ | C. | $\vec a$ | D. | $\vec b$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com