
【题目】如图,在三棱锥![]() 中,底面是边长为4的正三角形,
中,底面是边长为4的正三角形,![]() 底面
底面![]() ,点
,点![]() 分别为
分别为![]() 的中点,且异面直线
的中点,且异面直线![]() 和
和![]() 所成的角的大小为
所成的角的大小为![]() .
.
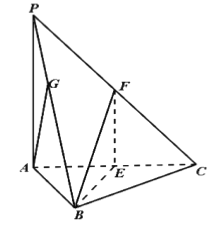
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求三棱锥![]() 的体积.
的体积.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】为了坚决打赢新冠状病毒的攻坚战,阻击战,某小区对小区内的![]() 名居民进行模排,各年龄段男、女生人数如下表.已知在小区的居民中随机抽取
名居民进行模排,各年龄段男、女生人数如下表.已知在小区的居民中随机抽取![]() 名,抽到
名,抽到![]() 岁~
岁~![]() 岁女居民的概率是
岁女居民的概率是![]() .现用分层抽样的方法在全小区抽取
.现用分层抽样的方法在全小区抽取![]() 名居民,则应在
名居民,则应在![]() 岁以上抽取的女居民人数为( )
岁以上抽取的女居民人数为( )
|
|
| |
女生 |
|
|
|
男生 |
|
|
|
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知圆心![]() 在直线
在直线![]() 上的圆
上的圆![]() 经过点
经过点![]() ,但不经过坐标原点,并且直线
,但不经过坐标原点,并且直线![]() 与圆
与圆![]() 相交所得的弦长为4.
相交所得的弦长为4.
(1)求圆![]() 的一般方程;
的一般方程;
(2)若从点![]() 发出的光线经过
发出的光线经过![]() 轴反射,反射光线刚好通过圆
轴反射,反射光线刚好通过圆![]() 的圆心,求反射光线所在的直线方程(用一般式表达).
的圆心,求反射光线所在的直线方程(用一般式表达).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,三国时代数学家赵爽在《周髀算经》中利用弦图,给出了勾股定理的绝妙证明.图中包含四个全等的直角三角形及一个小正方形(阴影),设直角三角形有一内角为![]() ,若向弦图内随机抛掷500颗米粒(大小忽略不计,取
,若向弦图内随机抛掷500颗米粒(大小忽略不计,取![]() ),则落在小正方形(阴影)内的米粒数大约为( )
),则落在小正方形(阴影)内的米粒数大约为( )
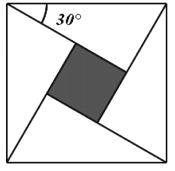
A. 134 B. 67 C. 200 D. 250
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】郴州市某中学从甲乙两个教师所教班级的学生中随机抽取100人,每人分别对两个教师进行评分,满分均为100分,整理评分数据,将分数以10为组距分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .得到甲教师的频率分布直方图,和乙教师的频数分布表:
.得到甲教师的频率分布直方图,和乙教师的频数分布表:

(1)在抽样的100人中,求对甲教师的评分低于70分的人数;
(2)从对乙教师的评分在![]() 范围内的人中随机选出2人,求2人评分均在
范围内的人中随机选出2人,求2人评分均在![]() 范围内的概率;
范围内的概率;
(3)如果该校以学生对老师评分的中位数是否大于80分作为衡量一个教师是否可评为该年度该校优秀教师的标准,则甲、乙两个教师中哪一个可评为年度该校优秀教师?(精确到0.1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了对某课题进行研究,分别从A,B,C三所高校中用分层随机抽样法抽取若干名教授组成研究小组,其中高校A有m名教授,高校B有72名教授,高校C有n名教授(其中![]() )
)
(1)若A,B两所高校中共抽取3名教授,B,C两所高校中共抽取5名教授,求m,n;
(2)若高校B中抽取的教授数是高校A和C中抽取的教授总数的![]() ,求三所高校的教授的总人数.
,求三所高校的教授的总人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年8月教育部、国家卫生健康委员会等八个部门联合印发《综合防控儿童青少年近视实话方案》中明确要求,为切实加强新时代儿童青少年近视防控工作,学校应严格组织全体学生每天上、下午各大做1次眼保健操.为了了解学校推广眼保健操是否能有效预防近视,随机从甲学校抽取了50名学生,再从乙学校选出与甲学校被抽取的50名学生视力情况一样的50学生(期中甲学校每天安排学生做眼保健操,乙学校不安排做跟保健操),一段时间后检测他们的视力情况并统计,若视力情况为1.0及以上,则认为该学生视力良好,否则认为该学生的视力一般,表1为甲学校视力情况的频率分布表,表2为乙学校学生视力情况的频率分布表,根据表格回答下列问题:
表1 甲学校学生视力情况的频率分布表
视力情况 | 0.6 | 0.8 | 1.0 | 1.2 | 1.5 |
频 数 | 1 | 1 | 15 | 15 | 18 |
表2 乙学校学生视力情况的频率分布表
视力情况 | 0.5 | 0.6 | 0.8 | 1.0 | 1.2 | 1.5 |
频 数 | 2 | 2 | 4 | 19 | 13 | 10 |
(1)求在甲学校的50名学生中随机选择1名同学,求其视力情况为良好的概率;
(2)根据表1,表2,对在学校推广眼保健操的必要性进行分析;
(3)在乙学校视力情况一般的学生中选择2人,了解其具体用眼习惯,求这两人视力情况都为0.8的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的展开式中各项系数的和为2,则下列结论正确的有( )
的展开式中各项系数的和为2,则下列结论正确的有( )
A.![]()
B.展开式中常数项为160
C.展开式系数的绝对值的和1458
D.若![]() 为偶数,则展开式中
为偶数,则展开式中![]() 和
和![]() 的系数相等
的系数相等
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com