
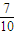 ,甲执白棋对乙的胜率为
,甲执白棋对乙的胜率为 .
.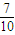 ,甲执白棋对乙的胜率为
,甲执白棋对乙的胜率为 ,利用互斥事件的概率公式,可求乙在一局比赛中获胜的概率;
,利用互斥事件的概率公式,可求乙在一局比赛中获胜的概率;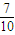 ,甲执白棋对乙的胜率为
,甲执白棋对乙的胜率为 .
.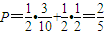 …(5分)
…(5分)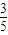 ,则
,则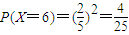 …(6分)
…(6分)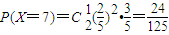 …(7分)
…(7分)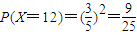 …(8分)
…(8分)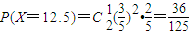 …(9分)
…(9分)| X | 6 | 7 | 12 | 12.5 |
| P | 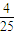 | 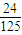 |  | 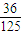 |
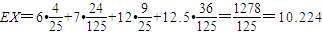 …..(12分)
…..(12分)

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
| 7 |
| 10 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:江西省上饶市2012届高三第一次高考模拟考试数学理科试题 题型:044
围棋对局中,执黑棋者先下,执白棋者后下.一次围棋比赛中,甲乙进入最后的冠军争夺战,决赛规则是三局两胜制(即三局比赛中,谁先赢得两局,就获得冠军),假定每局比赛没有平局,且每局比赛由裁判扔硬币决定谁执黑棋.根据甲乙双方以往对局记录,甲执黑棋对乙的胜率为![]() ,甲执白棋对乙的胜率为
,甲执白棋对乙的胜率为![]()
(1)求乙在一局比赛中获胜的概率;
(2)若冠军获得奖金10万元,亚军获得奖金5万元,且每局比赛胜方获得奖金1万元,负方获得奖金0.5万元,记甲在决赛中获得奖金数为X万元.求X的分布列和期望EX.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 ,甲执白棋对乙的胜率为
,甲执白棋对乙的胜率为 .
.查看答案和解析>>
科目:高中数学 来源: 题型:
设每堆棋子数目为n,你可以先试试能证明上述结论吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com