
设f(x)=x2+px+q,A={x|x=f(x)},B={x|x=f[f(x)]}.
(1)求证:A![]() B.
B.
(2)如果A={-1,3},求B.
科目:高中数学 来源:天利38套《2008全国各省市高考模拟试题汇编 精华大字版》、数学理 题型:022
设F为抛物线y=-![]() x2的焦点,与抛物线相切于点P(-4,-4)的直线l与x轴的交点为Q,则∠PQF=________.
x2的焦点,与抛物线相切于点P(-4,-4)的直线l与x轴的交点为Q,则∠PQF=________.
查看答案和解析>>
科目:高中数学 来源:云南省昆明一中2010届高三上学期期中考试数学理科试题 题型:022
设F为抛物线y=-![]() x2的焦点,与抛物线相切于点P(-4,-4)的直线l与x轴的交点为Q,∠PQF=________.
x2的焦点,与抛物线相切于点P(-4,-4)的直线l与x轴的交点为Q,∠PQF=________.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年广西省高三第二次模拟考试文科数学试卷 题型:填空题
设F为抛物线y=-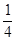 x2的焦点,与抛物线相切于点P(
x2的焦点,与抛物线相切于点P(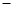 4,
4,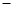 4)的直线l与x轴的交点为Q,则∠PQF的值是
4)的直线l与x轴的交点为Q,则∠PQF的值是
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数![]() 。
。
(I)求f(x)的单调区间;
(II)若对任意x∈[1,e],使得g(x)≥-x2+(a+2)x恒成立,求实数a的取值范围;
(III)设F(x)=![]() ,曲线y=F(x)上是否总存在两点P,Q,使得△POQ是以O(O为坐标原点)为钝角柄点的钝角三角开,且最长边的中点在y轴上?请说明理由。
,曲线y=F(x)上是否总存在两点P,Q,使得△POQ是以O(O为坐标原点)为钝角柄点的钝角三角开,且最长边的中点在y轴上?请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com