
(本小题13分)已知函数f(x)=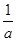 -
-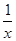 (a>0,x>0).
(a>0,x>0).
(1)求证:f(x)在(0,+∞)上是单调递增函数;
(2)若f(x)在[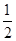 ,2]上的值域是[
,2]上的值域是[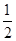 ,2],求a的值.
,2],求a的值.
(1)证明:见解析;(2) a=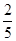 .
.
【解析】本事主要是考查了函数的单调性和函数值域的求解的综合运用。
(1)先分析函数的定义域内任意两个变量,代入函数解析式中作差,然后变形定号,下结论。
(2)∵f(x)在[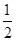 ,2]上的值域是[
,2]上的值域是[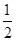 ,2],那么可知又f(x)在[
,2],那么可知又f(x)在[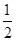 ,2]上单调递增,可知最大值和最小值在端点值取得求解得到参数a的值。
,2]上单调递增,可知最大值和最小值在端点值取得求解得到参数a的值。
解:(1)证明:设x2>x1>0,则x2-x1>0,x1x2>0.
∵f(x2)-f(x1)=(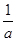 -
-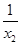 )-(
)-( 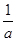 -
-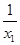 )=
)=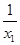 -
-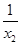
=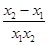 >0,
>0,
∴f(x2)>f(x1),∴f(x)在(0,+∞)上是单调递增的.………………6分
(2)∵f(x)在[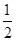 ,2]上的值域是[
,2]上的值域是[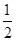 ,2],
,2],
又f(x)在[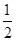 ,2]上单调递增,∴f(
,2]上单调递增,∴f(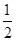 )=
)=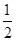 ,f(2)=2,
,f(2)=2,
易得a=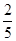 .
………………13分
.
………………13分


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源:2011-2012学年北京市示范校高三12月综合练习(一)文科数学 题型:解答题
(本小题13分)
已知等比数列 满足
满足 ,且
,且 是
是 ,
, 的等差中项.
的等差中项.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)若 ,
, ,求使
,求使
 成立的正整数
成立的正整数 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源:2011年福建省高一上学期期末考试数学理卷 题型:解答题
(本小题13分)
已知直线 过直线
过直线 和
和 的交点;
的交点;
(Ⅰ)若直线 与直线
与直线 垂直,求直线
垂直,求直线 的方程.
的方程.
(Ⅱ)若原点 到直线
到直线 的距离为1.求直线
的距离为1.求直线 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江西省协作体高三第二次联考数学理卷 题型:解答题
(本小题13分)
已知抛物线方程为 ,过
,过 作直线
作直线 .
.
①若 与
与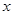 轴不垂直,交抛物线于A、B两点,是否存在
轴不垂直,交抛物线于A、B两点,是否存在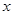 轴上一定点
轴上一定点 ,使得
,使得 ?若存在,求出m的值;若不存在,请说明理由?
?若存在,求出m的值;若不存在,请说明理由?
②若 与
与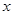 轴垂直,抛物线的任一切线与
轴垂直,抛物线的任一切线与 轴和
轴和 分别交于M、N两点,则自点M到以QN为直径的圆的切线长
分别交于M、N两点,则自点M到以QN为直径的圆的切线长 为定值,试证之;
为定值,试证之;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com