
【题目】比较下列各组中两个值的大小 :
(1)ln0.3,ln2; (2)loga3.1,loga5.2(a>0,且a≠1);
(3)log30.2,log40.2; (4)log3π,logπ3.
【答案】(1)ln0.3<ln2;(2)见解析;(3)log30.2<log40.2;(4)log3π>logπ3.
【解析】试题分析:(1)构造对数函数y=lnx,利用函数的单调性判断;(2)需对底数a分类讨化;(3)由于两个对数的底数不同,故不能直接比较大小,可对这两个对数分别取倒数,再根据同底对数函数的单调性比较大小;(4)构造对数函数,并借助中间量判断.
试题解析:
(1)因为函数y=lnx是增函数,且0.3<2,
所以ln0.3<ln2.
(2)当a>1时,函数y=logax在(0,+∞)上是增函数,
又3.1<5.2,所以loga3.1<loga5.2;
当0<a<1时,函数y=logax在(0,+∞)上是减函数,
又3.1<5.2,所以loga3.1>loga5.2.
(3)因为0>log0.23>log0.24,所以![]() <
<![]() ,即log30.2<log40.2.
,即log30.2<log40.2.
(4)因为函数y=log3x是增函数,且π>3,所以log3π>log33=1,
同理,1=logππ>logπ3,即log3π>logπ3.


 步步高达标卷系列答案
步步高达标卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为自然对数的底数,
为自然对数的底数,![]() ),
),![]() (
(![]() ,
,![]()
![]() ),
),
⑴若![]() ,
,![]() .求
.求![]() 在
在![]() 上的最大值
上的最大值![]() 的表达式;
的表达式;
⑵若![]() 时,方程
时,方程![]() 在
在![]() 上恰有两个相异实根,求实根
上恰有两个相异实根,求实根![]() 的取值范围;
的取值范围;
⑶若![]() ,
,![]() ,求使
,求使![]() 得图像恒在
得图像恒在![]() 图像上方的最大正整数
图像上方的最大正整数![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题:①集合![]() 的子集个数有16个;②定义在
的子集个数有16个;②定义在![]() 上的奇函数
上的奇函数![]() 必满足
必满足![]() ;③
;③![]() 既不是奇函数又不是偶函数;④偶函数的图像一定与
既不是奇函数又不是偶函数;④偶函数的图像一定与![]() 轴相交;⑤
轴相交;⑤![]() 在
在![]() 上是减函数。
上是减函数。
其中真命题的序号是 ______________(把你认为正确的命题的序号都填上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前3项和为6,前8项和为-4.
(1)求数列{an}的通项公式;
(2)设bn=(4-an)qn-1 (q≠0,n∈N*),求数列{bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线y2=2px(p>0)的焦点为F,A是抛物线上横坐标为4,且位于x轴上方的点,A到抛物线准线的距离等于5,过A作AB垂直于y轴,垂足为B,OB的中点为M.
(1)求抛物线的方程;
(2)以M为圆心,MB为半径作圆M,当K(m,0)是x轴上一动点时,讨论直线AK与圆M的位置关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①若(1-x)5=a0+a1x+a2x2+a3x3+a4x4+a5x5,则|a1|+|a2|+|a3|+|a4|+|a5|=32
②α,β,γ是三个不同的平面,则“γ⊥α,γ⊥β”是“α∥β”的充分条件
③已知sin![]() =
=![]() ,则cos
,则cos![]() =
=![]() .其中正确命题的个数为( )
.其中正确命题的个数为( )
A.0 B.1
C.2 D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】东莞市某高级中学在今年4月份安装了一批空调,关于这批空调的使用年限![]() (单位:年,
(单位:年, ![]() )和所支出的维护费用
)和所支出的维护费用![]() (单位:万元)厂家提供的统计资料如下:
(单位:万元)厂家提供的统计资料如下:

(1)请根据以上数据,用最小二乘法原理求出维护费用![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若规定当维护费用![]() 超过13.1万元时,该批空调必须报废,试根据(1)的结论求该批空调使用年限的最大值.
超过13.1万元时,该批空调必须报废,试根据(1)的结论求该批空调使用年限的最大值.
参考公式:最小二乘估计线性回归方程![]() 中系数计算公式:
中系数计算公式:
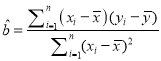 ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为(-2,2),函数g(x)=f(x-1)+f(3-2x).
(1)求函数g(x)的定义域;
(2)若f(x)是奇函数,且在定义域上单调递减,求不等式g(x)≤0的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com