
【题目】3个红球与3个黑球随机排成一行,从左到右依次在球上标记1,2,3,4,5,6,则红球上的数字之和小于黑球上的数字之和的概率为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
【答案】D
【解析】
将红球与黑球上标记数字情况用表格列举,
根据表格可知“红球上数字之和小于黑球上数字之和”与“红球上数字之和大于黑球上数字之和”是“对等”的,即可得出概率为.
解:红球与黑球上标记数字情况用表格列举如下:
红球 | 1,2,3 | 1,2,4 | 1,2,5 | 1,2,6 | 1,3,4 | 1,3,5 | 1,3,6 | 1,4,5 | 1,4,6 | 1,5,6 | 黑球 |
黑球 | 4,5,6 | 3,5,6 | 3,4,6 | 3,4,5 | 2,5,6 | 2,4,6 | 2,4,5 | 2,3,6 | 2,3,5 | 2,3,4 | 红球 |
共![]() 种情况,红球与黑球上数字之和均不相等,红球上数字之和小于黑球上数字之和与红球上数字之和大于黑球上数字之和是“对等”的,各占一半,故所求概率为
种情况,红球与黑球上数字之和均不相等,红球上数字之和小于黑球上数字之和与红球上数字之和大于黑球上数字之和是“对等”的,各占一半,故所求概率为![]() ,故选D.
,故选D.


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,底面
,底面![]() 是直角梯形,其中
是直角梯形,其中![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为棱
为棱![]() 上的点,且
上的点,且![]() .
.
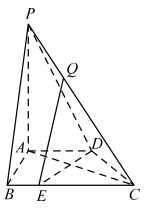
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)设![]() 为棱
为棱![]() 上的点(不与
上的点(不与![]() ,
,![]() 重合),且直线
重合),且直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 长轴长为短轴长的两倍,连结椭圆的四个顶点得到的菱形的面积为4,直线
长轴长为短轴长的两倍,连结椭圆的四个顶点得到的菱形的面积为4,直线![]() 过点
过点![]() ,且与椭圆相交于另一点
,且与椭圆相交于另一点![]() .
.
(1)求椭圆的方程;
(2)若线段![]() 长为
长为![]() ,求直线
,求直线![]() 的倾斜角;
的倾斜角;
(3)点![]() 在线段
在线段![]() 的垂直平分线上,且
的垂直平分线上,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,斜率为1的直线与椭圆
,斜率为1的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,其中
,其中![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设过点![]() 且与直线
且与直线![]() 平行的直线与椭圆
平行的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,若点
两点,若点![]() 满足
满足![]() ,且
,且![]() 与椭圆
与椭圆![]() 的另一个交点为
的另一个交点为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的一个焦点为
的一个焦点为![]() ,离心率为
,离心率为![]() .
.
(1)求![]() 的标准方程;
的标准方程;
(2)若动点![]() 为
为![]() 外一点,且
外一点,且![]() 到
到![]() 的两条切线相互垂直,求
的两条切线相互垂直,求![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(3)设![]() 的另一个焦点为
的另一个焦点为![]() ,过
,过![]() 上一点
上一点![]() 的切线与(2)所求轨迹
的切线与(2)所求轨迹![]() 交于点
交于点![]() ,
,![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】实数a,b满足ab>0且a≠b,由a、b、![]() 、
、![]() 按一定顺序构成的数列( )
按一定顺序构成的数列( )
A. 可能是等差数列,也可能是等比数列
B. 可能是等差数列,但不可能是等比数列
C. 不可能是等差数列,但可能是等比数列
D. 不可能是等差数列,也不可能是等比数列
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在圆台![]() 中,平面
中,平面![]() 过上下底面的圆心
过上下底面的圆心![]() ,
,![]() ,点M在
,点M在![]() 上,N为
上,N为![]() 的中点,
的中点,![]() .
.
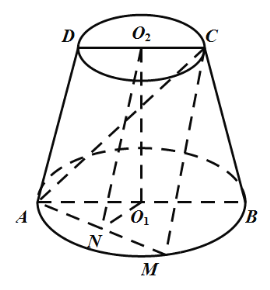
(1)求证:平面![]() 平面
平面![]() ;
;
(2)当![]() 时,
时,![]() 与底面
与底面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义域为R的函数![]() ,若函数
,若函数![]() 是奇函数,则称
是奇函数,则称![]() 为正弦奇函数.已知
为正弦奇函数.已知![]() 是单调递增的正弦奇函数,其值域为R,
是单调递增的正弦奇函数,其值域为R,![]() .
.
(1)已知![]() 是正弦奇函数,证明:“
是正弦奇函数,证明:“![]() 为方程
为方程![]() 的解”的充要条件是“
的解”的充要条件是“![]() 为方程
为方程![]() 的解”;
的解”;
(2)若![]()
![]() ,求
,求![]() 的值;
的值;
(3)证明:![]() 是奇函数.
是奇函数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com