
已知定义在R上的函数f(x)=lg(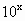 +1)+3x
+1)+3x
(1)设g(x)是R上的奇函数,h(x)是R上的偶函数,且满足f(x)=g(x)+h(x),试求g(x)与h(x);
(2)设a、b∈R,证明a+b>0是f(a)+f(b)>f(-a)+f(-b)的充分必要条件.
|
(1)由f(x)=g(x)+h(x) ∴f(-x)=g(-x)+h(-x). ∵g(x)是奇函数,h(x)是偶函数 ∴f(-x)=-g(x)+h(x) ∴g(x)= g(x)= = = = = h(x)=f(x)-g(x)= (2)任取
∵
∴ 即f(x)是定义域R上的增函数. 由a+b>0,∴a>-b,b>-a. ∴f(a)>f(-b),f(b)>f(-a),将两式相加 ∴f(a)+f(b)>f(-a)+f(-b) 即a+b>0是f(a)+f(b)>f(-a)+f(-b)成立的充分条件. 由f(a)+f(b)>f(-a)+f(-b), ∴g(a)+h(a)+g(b)+h(b)>g(-a)+h(-a)+g(-b)+h(-b). ∵g(a)是奇函数,h(x)是偶函数, ∴g(a)+h(a)+g(b)+h(b)>-g(a)+h(a)-g(b)+h(b). ∴2[g(a)+g(b)]>0. ∴ 即f(a)+f(b)>f(-a)+f(-b)是a+b>0成立的必要条件. 综上,a+b>0是f(a)+f(b)>f(-a)+f(-b)成立的充分必要条件. |


 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、-2 | B、2 | C、4 | D、-4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、0 | B、2013 | C、3 | D、-2013 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com