
【题目】已知函数![]() ,
, ![]() .
.
(![]() )若
)若![]() ,求曲线
,求曲线![]() 在点
在点![]() 处的切线方程.
处的切线方程.
(![]() )若
)若![]() ,求函数
,求函数![]() 的单调区间.
的单调区间.
(![]() )若
)若![]() ,且
,且![]() 在区间
在区间![]() 上恒成立,求
上恒成立,求![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别为A,B,C所对边,a+b=4,(2﹣cosA)tan ![]() =sinA.
=sinA.
(1)求边长c的值;
(2)若E为AB的中点,求线段EC的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,上顶点为
,上顶点为![]() ,若直线
,若直线![]() 的斜率为1,且与椭圆的另一个交点为
的斜率为1,且与椭圆的另一个交点为![]() ,
, ![]() 的周长为
的周长为![]() .
.
(1)求椭圆的标准方程;
(2)过点![]() 的直线
的直线![]() (直线
(直线![]() 的斜率不为1)与椭圆交于
的斜率不为1)与椭圆交于![]() 两点,点
两点,点![]() 在点
在点![]() 的上方,若
的上方,若![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角梯形ABCD中,AD∥BC,∠A=90°,AB=2AD,若将△ABD沿直线BD折成△A′BD,使得A′D⊥BC,则直线A′B与平面BCD所成角的正弦值是 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 向量 ![]() =(Sn , 1),
=(Sn , 1), ![]() =(2n﹣1,
=(2n﹣1, ![]() ),满足条件
),满足条件 ![]() ∥
∥ ![]() ,
,
(1)求数列{an}的通项公式,
(2)设函数f(x)=( ![]() )x , 数列{bn}满足条件b1=1,f(bn+1)=
)x , 数列{bn}满足条件b1=1,f(bn+1)= ![]() .
.
①求数列{bn}的通项公式,
②设cn= ![]() ,求数列{cn}的前n项和Tn .
,求数列{cn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线的顶点是坐标原点![]() ,焦点
,焦点![]() 在
在![]() 轴的正半轴上,过焦点
轴的正半轴上,过焦点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与抛物线交于
与抛物线交于![]() 两点,且满足
两点,且满足![]() .
.
(1)求抛物线的方程;
(2)已知![]() 为抛物线上一点,若点
为抛物线上一点,若点![]() 位于
位于![]() 轴下方且
轴下方且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来城市“共享单车”的投放在我国各地迅猛发展,“共享单车”为人们出行提供了很大的便利,但也给城市的管理带来了一些困难,现某城市为了解人们对“共享单车”投放的认可度,对![]() 年龄段的人群随机抽取
年龄段的人群随机抽取![]() 人进行了一次“你是否赞成投放共享单车”的问卷调查,根据调查结果得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次“你是否赞成投放共享单车”的问卷调查,根据调查结果得到如下统计表和各年龄段人数频率分布直方图:
组号 | 分组 | 赞成投放的人数 | 赞成投放的人数占本组的频率 |
第一组 |
|
|
|
第二组 |
|
|
|
第三组 |
|
|
|
第四组 |
|
|
|
第五组 |
|
|
|
第六组 |
|
|
|
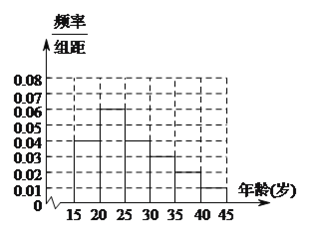
(![]() )求
)求![]() ,
, ![]() ,
, ![]() 的值.
的值.
(![]() )在第四、五、六组“赞成投放共享单车”的人中,用分层抽样的方法抽取
)在第四、五、六组“赞成投放共享单车”的人中,用分层抽样的方法抽取![]() 人参加“共享单车”骑车体验活动,求第四、五、六组应分别抽取的人数.
人参加“共享单车”骑车体验活动,求第四、五、六组应分别抽取的人数.
(![]() )在(
)在(![]() )中抽取的
)中抽取的![]() 人中随机选派
人中随机选派![]() 人作为领队,求所选派的
人作为领队,求所选派的![]() 人中第五组至少有一人的概率.
人中第五组至少有一人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两人同时生产内径为![]() 的一种零件,为了对两人的生产质量进行评比,从他们生产的零件中各抽出 5 件(单位:
的一种零件,为了对两人的生产质量进行评比,从他们生产的零件中各抽出 5 件(单位: ![]() ) ,
) ,
甲:25.44,25.43, 25.41,25.39,25.38
乙:25.41,25.42, 25.41,25.39,25.42.
从生产的零件内径的尺寸看、谁生产的零件质量较高.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com