练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】现安排甲乙丙丁戊5名学生分别担任语文、数学、英语、物理、化学学科的科代表，要求甲不当语文科代表，乙不当数学科代表，若丙当物理科代表则丁必须当化学科代表，则不同的选法共有多少种( )

    A. 53 B. 67 C. 85 D. 91

    【答案】B

    【解析】丙当物理课代表则丁必须当化学课代表，以丙进行分类 第一类，当丙当物理课代表时，丁必须当化学课代表，再根据甲当数学课代表，乙戊可以当英语和语文中的任一课，有种，当甲不当数学课代表，甲只能当英语课代表，乙只能当语文课代表，戊当数学课代表，有种，共计种， 第二类，当丙不当物理课代表时，分四类①丙为语文课代表时，乙只能从英语、物理和U学中选择一课，剩下的甲丁戊任意排给剩下的三
    课，有种，②丙为数学课代表时，甲只能从英语、物理和化学课，剩下的乙丁戊任意排给剩下的三课，有种，③丙为英语课代表时，继续分类，甲当数学课代表时，其他三位同学任意当有种，当甲不当数学课代表，甲只能从物理和化学课中选一课,乙只能从语文和甲选完后的剰下的一课中选一课，丁和戊做剰下的两课，有,共计种④丙为化学课代表时，同③的选法一样有种，根据分类计数原理得，不同的选法共有故选.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数（）.

    （1）是否存在实数使函数是奇函数？并说明理由；

    （2）在（1）的条件下，当时， 恒成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的离心率,以上顶点和右焦点为直径端点的圆与直线相切．

    (1)求椭圆的标准方程；

    (2)对于直线和点,椭圆上是否存在不同的两点与关于直线对称,且,若存在实数的值,若不存在,说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，其中且，若， 在处切线的斜率为．

    （1）求函数的解析式及其单调区间；

    （2）若实数满足，且对于任意恒成立，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱锥中，平面 平面， ， 且， ， 分别为， 的中点.

    （1）求证： 平面；

    （2）求证：平面 平面；

    （3）求三棱锥的体积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在刚刚结束的五市联考中，某校对甲、乙两个文科班的数学成绩进行分析，规定：大于或等于120分为优秀，120分以下为非优秀，成绩统计后，得到如下的列联表，且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为.

    班级

    优秀

    非优秀

    合计

    甲班

    18

    乙班

    43

    合计

    110

    (1)请完成上面的列联表；

    (2)请问：是否有的把握认为“数学成绩与所在的班级有关系”？

    (3)用分层抽样的方法从甲、乙两个文科班的数学成绩优秀的学生中抽取5名学生进行调研，然后再从这5名学生中随机抽取2名学生进行谈话，求抽到的2名学生中至少有1名乙班学生的概率.

    参考公式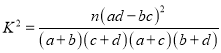： (其中)

    参考数据：

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校的一个社会实践调查小组，在对该校学生的良好“用眼习惯”的调查中，随机发放了120分问卷.对收回的100份有效问卷进行统计，得到如下列联表：

    做不到科学用眼

    能做到科学用眼

    合计

    男

    45

    10

    55

    女

    30

    15

    45

    合计

    75

    25

    100

    （1）现按女生是否能做到科学用眼进行分层，从45份女生问卷中抽取了6份问卷，从这6份问卷中再随机抽取3份，并记其中能做到科学用眼的问卷的份数，试求随机变量的分布列和数学期望；

    （2）若在犯错误的概率不超过的前提下认为良好“用眼习惯”与性别有关，那么根据临界值表，最精确的的值应为多少？请说明理由.

    附：独立性检验统计量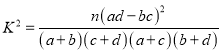，其中.

    独立性检验临界值表：

    0.25

    0.15

    0.10

    0.05

    0.025

    1.323

    2.072

    2.706

    3.840

    5.024

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在某校歌咏比赛中，甲班、乙班、丙班、丁班均可从、、、四首不同曲目中任选一首.

    （1）求甲、乙两班选择不同曲目的概率；

    （2）设这四个班级总共选取了首曲目，求的分布列及数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在一次抗洪抢险中，准备用射击的方法引爆从桥上游漂流而下的一个巨大的汽油灌，已知只有5发子弹，第一次命中只能使汽油流出，第二次命中才能引爆．每次射击相互独立，且命中概率都是，求（1）油罐被引爆的概率；（2）如果引爆或子弹打光则停止射击，设射击次数为，求的分布列．

    查看答案和解析>>

    同步练习册答案