
如图,PA为⊙O的切线,A为切点,PBC是过点O的割线,PA=10,PB=5。
求:(1)⊙O的半径;(2)s1n∠BAP的值。
(1)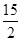 ;(2)
;(2) .
.
解析试题分析:(1)由 为圆
为圆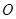 的切线,可得出
的切线,可得出 为弦切角,根据弦切角等于夹弧所对的圆周角,可得出
为弦切角,根据弦切角等于夹弧所对的圆周角,可得出 ,再由
,再由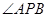 与
与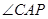 为公共角,根据两对对应角相等的两三角形相似,可得出
为公共角,根据两对对应角相等的两三角形相似,可得出 与
与 相似,根据相似三角形成比例列出比例式,将
相似,根据相似三角形成比例列出比例式,将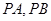 的值代入,求出
的值代入,求出 的长,再由
的长,再由 求出直径
求出直径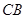 的长,进而确定出半径的值;
的长,进而确定出半径的值;
(2) ,故要求
,故要求 ,即要求
,即要求 ,由
,由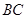 为直径,根据直径所对的圆周角为直角,可得出
为直径,根据直径所对的圆周角为直角,可得出 为直角三角形,根据锐角三角函数定义,
为直角三角形,根据锐角三角函数定义,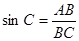 ,由第一问得出的三角形相似,用对应边
,由第一问得出的三角形相似,用对应边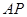 比
比 求出相似三角形的对应边之比为
求出相似三角形的对应边之比为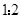 ,可设
,可设 ,则有
,则有 ,在
,在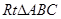 中,根据勾股定理可列出关于
中,根据勾股定理可列出关于 的方程,求出方程的解得到
的方程,求出方程的解得到 的值,确定出
的值,确定出 的长,即可求出
的长,即可求出 的值,即为
的值,即为 的值.
的值.
试题解析:(1)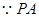 为圆
为圆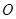 的切线,
的切线,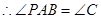 ,又
,又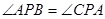 ,
,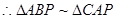 ,
, ,即
,即 ,
,
又 ,
, ,即
,即
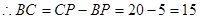 ,
,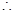 圆的半径
圆的半径 ;
;
(2)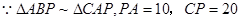 ,
,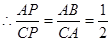
设 ,则
,则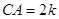 ,
,
又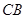 为圆
为圆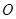 的直径,
的直径,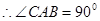 ,
,
在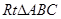 中,根据勾股定理得:
中,根据勾股定理得: ,
,
解得:
 ,
,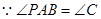 ,
,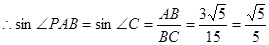
考点:1.切线的性质;2.相似三角形的判定与性质.


科目:高中数学 来源: 题型:解答题
如图,已知C点在圆O直径BE的延长线上,CA切圆O于A点,DC是∠ACB的平分线交AE于点F,交AB于D点.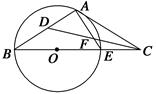
(1)求∠ADF的度数;
(2)AB=AC,求AC∶BC.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在梯形ABCD中,AD∥BC,AC⊥BD,垂足为E,∠ABC=45°,过E作AD的垂线交AD于F,交BC于G,过E作AD的平行线交AB于H.求证:FG2=AF·DF+BG·CG+AH·BH.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,已知A、B、C三点的坐标分别为(0,1)、(-1,0)、(1,0),P是线段AC上一点,BP交AO于点D,设三角形ADP的面积为S,点P的坐标为(x,y),求S关于x的函数表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在锐角三角形ABC中,D 为C在AB上的射影,E 为D在BC上的射影,F为DE上一点,且满足

(1)证明: (2)若AD=2,CD=3.DB=4,求
(2)若AD=2,CD=3.DB=4,求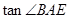 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,已知△ABC中的两条角平分线AD和CE相交于H,∠B=60°,F在AC上,且AE=AF.
(1)证明:B,D,H,E四点共圆;
(2)证明:CE平分∠DEF.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在△ABC中,延长BC到D,使CD=BC,取AB的中点F,连接FD交AC于点E.
(1)求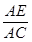 的值;
的值;
(2)若AB=a,FB=EC,求AC的长.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在矩形ABCD中,AB> ·AD,E为AD的中点,连结EC,作EF⊥EC,且EF交AB于F,连结FC.设
·AD,E为AD的中点,连结EC,作EF⊥EC,且EF交AB于F,连结FC.设 =k,是否存在实数k,使△AEF、△ECF、△DCE与△BCF都相似?若存在,给出证明;若不存在,请说明理由.
=k,是否存在实数k,使△AEF、△ECF、△DCE与△BCF都相似?若存在,给出证明;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com