
分析 (1)车费f(x)与路程x的关系式为f(x)=$\left\{\begin{array}{l}{5,0<x≤3}\\{5+(x-3)×1.2,3<x≤10}\\{5+7×1.2+(x-10)×1.8,x>10}\end{array}\right.$.
(2)30公里不换车的车费为1.8×30-4.6=49.4(元);分别计算方案①:行驶两个15公里的车费为
(1.8×15-4.6)×2;方案②:行三个10公里的车费为(1.2×10+1.4)×3,半径即可得出.
解答 解:(1)车费f(x)与路程x的关系式为:
f(x)=$\left\{\begin{array}{l}{5,0<x≤3}\\{5+(x-3)×1.2,3<x≤10}\\{5+7×1.2+(x-10)×1.8,x>10}\end{array}\right.$,
即f(x)=$\left\{\begin{array}{l}{5,0<x≤3}\\{1.2x+1.4,3<x≤10}\\{1.8x-4.6,x>10}\end{array}\right.$.
(2)30公里不换车的车费为1.8×30-4.6=49.4(元);
方案①:行驶两个15公里的车费为:
(1.8×15-4.6)×2=44.8(元);
方案②:行三个10公里的车费为:
(1.2×10+1.4)×3=40.2(元).
由此可见,方案①和方案②都比不换车省钱,方案②比方案①更省钱.
点评 本题考查了分段函数的单调性、分类讨论方法,考查了推理能力与计算能力,属于中档题.


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
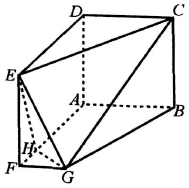 在多面体ABCDEFG中,四边形ABCD与ADEF是边长均为a的正方形,四边形ABGH是直角梯形,AB⊥AF,且FA=2FG=4FH.
在多面体ABCDEFG中,四边形ABCD与ADEF是边长均为a的正方形,四边形ABGH是直角梯形,AB⊥AF,且FA=2FG=4FH.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com