

(1)设点O是AB的中点,证明OC∥平面A1B1C1;
(2)求AB与平面AA1C1C所成的角的大小;
(3)求此几何体的体积.
解法一:(1)证明:作OD∥AA1交A1B1于D,连结C1D.
则OD∥BB1∥CC1.
因为O是AB的中点,
所以OD=![]() (AA1+BB1)=3=CC1.
(AA1+BB1)=3=CC1.
则ODC1C是平行四边形,因此有OC∥C1D,
C1D![]() 平面C1B1A1且OC
平面C1B1A1且OC![]() 平面C1B1A1,则OC∥面A1B1C1.
平面C1B1A1,则OC∥面A1B1C1.
(2)解:如图,过B作截面BA2C2∥面A1B1C1,分别交AA1、CC1于A2、C2,

作BH⊥A2C2于H.
因为平面A2BC2⊥平面AA1C1C,则BH⊥面AA1C1C.
连结AH,则∠BAH就是AB与面AA1C1C所成的角.
因为BH=![]() ,AB=
,AB=![]() ,
,
所以sin∠BAH=![]() ,
,
AB与面AA1C1C所成的角为∠BAH=arcsin![]() .
.
(3)解:因为BH=![]() ,
,
所以VB—AA2C2C=![]() SAA2C2C·BH=
SAA2C2C·BH=![]() ·
·![]() (1+2)·
(1+2)·![]() ·
·![]() =
=![]() ,
,
VA1B1C1—A2BC2=S△A1B1C1·BB1=![]() ·2=1.
·2=1.
所求几何体的体积为V=VB—AA2C2C+VA1B1C1—A2BC2=![]() .
.
解法二:
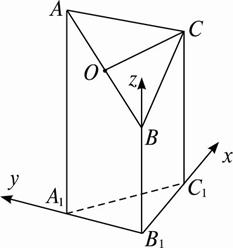
(1)证明:如图,以B1为原点建立空间直角坐标系,
则A(0,1,4),B(0,0,2),C(1,0,3),因为O是AB的中点,
所以O(0,![]() ,3),
,3),![]() =(1,-
=(1,-![]() ,0).
,0).
易知n=(0,0,1)是平面A1B1C1的一个法向量.
因为![]() ·n=0,OC
·n=0,OC![]() 平面A1B1C1,
平面A1B1C1,
所以OC∥平面A1B1C1.
(2)解:设AB与面AA1C1C所成的角为θ,
求得![]() =(0,0,4),
=(0,0,4),![]() =(1,-1,0).
=(1,-1,0).
设m=(x,y,z)是平面AA1C1C的一个法向量,则
由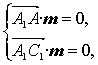
得![]()
取x=y=1,得m=(1,1,0).
又因为![]() =(0,-1,-2),
=(0,-1,-2),
所以cos〈m,![]() 〉=
〉=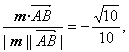
则sinθ=![]() .
.
所以AB与面AA1C1C所成的角为arcsin![]() .
.
(3)同解法一.绿色通道:
本题主要考查直线与平面平行的判定及直线与平面所成角及几何体体积的求法,解法一为传统解法,解法二为向量解法.两种方法各有千秋,充分体现了思维的灵活性.
在解决此类问题时,要注意计算方法的灵活性,特别是向量解法,应注意各点的坐标.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:
(07年江西卷文)(12分)
下图是一个直三棱柱(以![]() 为底面)被一平面所截得到的几何体,截面为
为底面)被一平面所截得到的几何体,截面为![]() .已知
.已知![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)设点![]() 是
是![]() 的中点,证明:
的中点,证明:![]() 平面
平面![]() ;
;
(2)求![]() 与平面
与平面![]() 所成的角的大小;
所成的角的大小;
(3)求此几何体的体积.

查看答案和解析>>
科目:高中数学 来源:江西省高考真题 题型:解答题

查看答案和解析>>
科目:高中数学 来源:江西省高考真题 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:

(1)设点O是AB的中点,证明:OC∥平面A1B1C1;
(2)求AB与平面AA1C1C所成的角的大小;
(3)求此几何体的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com