
【题目】对于函数f(x)=xlnx有如下结论: ①该函数为偶函数;
②若f′(x0)=2,则x0=e;
③其单调递增区间是[ ![]() ,+∞);
,+∞);
④值域是[ ![]() ,+∞);
,+∞);
⑤该函数的图象与直线y=﹣ ![]() 有且只有一个公共点.(本题中e是自然对数的底数)
有且只有一个公共点.(本题中e是自然对数的底数)
其中正确的是(请把正确结论的序号填在横线上)
【答案】②③⑤
【解析】解:f(x)=xlnx的定义域是(0,+∞),故不是偶函数,故①错误; f′(x)=lnx+1,令f′(x0)=2,即lnx0+1=2,解得:x0=e,故②正确;
令f'(x)>0,即lnx+1>0,
解得:x> ![]() ,
,
∴f(x)的单调递增区间是[ ![]() ,+∞),故③正确;
,+∞),故③正确;
由f(x)在(0, ![]() )递减,在(
)递减,在( ![]() ,+∞)递增,
,+∞)递增,
得:f(x)的最小值是f( ![]() )=﹣
)=﹣ ![]() ,
,
故f(x)的值域是[﹣ ![]() ,+∞),故④错误;
,+∞),故④错误;
故该函数的图象与直线y=﹣ ![]() 有且只有一个公共点,⑤正确;
有且只有一个公共点,⑤正确;
所以答案是:②③⑤.
【考点精析】根据题目的已知条件,利用利用导数研究函数的单调性的相关知识可以得到问题的答案,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:高中数学 来源: 题型:
【题目】如图所示,P是四边形ABCD所在平面外的一点,四边形ABCD是∠DAB=60°且边长为a的菱形.侧面PAD为正三角形,其所在平面垂直于底面ABCD.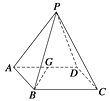
(1)若G为AD边的中点,求证:BG⊥平面PAD;
(2)求证:AD⊥PB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{bn}满足bn=| ![]() |,其中a1=2,an+1=
|,其中a1=2,an+1= ![]()
(1)求b1 , b2 , b3 , 并猜想bn的表达式(不必写出证明过程);
(2)设cn= ![]() ,数列|cn|的前项和为Sn , 求证Sn<
,数列|cn|的前项和为Sn , 求证Sn< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)的定义域为R,导函数f'(x)的图象如图所示,则函数f(x)( ) 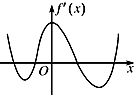
A.无极大值点,有四个极小值点
B.有三个极大值点,两个极小值点
C.有两个极大值点,两个极小值点
D.有四个极大值点,无极小值点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面α内有一以AB为直径的圆,PA⊥α,点C在圆周上移动(不与A,B重合),点D,E分别是A在PC,PB上的射影,则( )
A.∠ACD是二面角A﹣PC﹣B的平面角
B.∠AED是二面角A﹣PB﹣C的平面角
C.∠EDA是二面角A﹣PC﹣B的平面角
D.∠DAE是二面角B﹣PA﹣C的平面角
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴,建立极坐标系.已知曲线C1: ![]() (t为参数),C2:
(t为参数),C2: ![]() (θ为参数). (Ⅰ)化C1 , C2的方程为普通方程,并说明它们分别表示什么曲线;
(θ为参数). (Ⅰ)化C1 , C2的方程为普通方程,并说明它们分别表示什么曲线;
(Ⅱ)若C1上的点P对应的参数为t=﹣ ![]() ,Q为C2上的动点,求线段PQ的中点M到直线C3:ρcosθ﹣
,Q为C2上的动点,求线段PQ的中点M到直线C3:ρcosθ﹣ ![]() ρsinθ=8+2
ρsinθ=8+2 ![]() 距离的最小值.
距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】①设三个正实数a , b , c , 满足![]() ,求证:a , b , c一定是某一个三角形的三条边的长;
,求证:a , b , c一定是某一个三角形的三条边的长;
②设n个正实数 a1,a2,...an 满足不等式 ![]() (其中
(其中 ![]() ),求证: a1,a2,...an 中任何三个数都是某一个三角形的三条边的长.
),求证: a1,a2,...an 中任何三个数都是某一个三角形的三条边的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直线mx+ ![]() y﹣1=0在y轴上的截距是﹣1,且它的倾斜角是直线
y﹣1=0在y轴上的截距是﹣1,且它的倾斜角是直线 ![]() =0的倾斜角的2倍,则( )
=0的倾斜角的2倍,则( )
A.m=﹣ ![]() ,n=﹣2
,n=﹣2
B.m= ![]() ,n=2
,n=2
C.m= ![]() ,n=﹣2
,n=﹣2
D.m=﹣ ![]() ,n=2
,n=2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com