
【题目】在直角坐标系中,曲线C的参数方程为![]() 为参数),以原点为极点,x轴的正半轴为极轴,建立极坐标系,曲线D的极坐标方程为
为参数),以原点为极点,x轴的正半轴为极轴,建立极坐标系,曲线D的极坐标方程为![]() .
.
(1)写出曲线C的极坐标方程以及曲线D的直角坐标方程;
(2)若过点![]() (极坐标)且倾斜角为
(极坐标)且倾斜角为![]() 的直线l与曲线C交于M,N两点,弦MN的中点为P,求
的直线l与曲线C交于M,N两点,弦MN的中点为P,求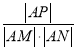 的值.
的值.
【答案】(1)曲线C的极坐标方程为![]() ;曲线D的直角坐标方程为
;曲线D的直角坐标方程为![]() ;(2)
;(2)![]() .
.
【解析】
(1)由曲线C的参数方程,利用三角函数的基本关系式,求得曲线C的普通方程,结合极坐标方程与直角坐标方程的互化公式,即可求得曲线C的极坐标方程和曲线D的直角坐标方程;
(2)根据题意,求得直线l的参数方程为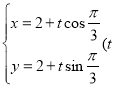 为参数),代入曲线C的方程,结合一元二次方程根与系数的关系得
为参数),代入曲线C的方程,结合一元二次方程根与系数的关系得![]() ,即可求解.
,即可求解.
(1)由题意,曲线C的参数方程为![]() 为参数),即
为参数),即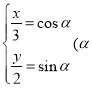 为参数)
为参数)
平方相加,可得曲线C的普通方程为![]() ,
,
将![]() 代入曲线C的普通方程
代入曲线C的普通方程
可得曲线C的极坐标方程为![]() ,
,
又由曲线D的极坐标方程为![]() ,
,
所以![]() ,
,
又由![]()
所以![]() ,
,
所以曲线C的极坐标方程为![]() ,
,
曲线D的直角坐标方程为![]() .
.
(2)由点![]() ,则
,则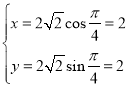 ,即点A(2,2).
,即点A(2,2).
因为直线l过点A(2,2)且倾斜角为![]() ,
,
所以直线l的参数方程为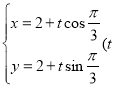 为参数),代入
为参数),代入![]() ,
,
可得![]() ,
,
设M,N对应的参数分别为![]() ,
,
由一元二次方程根与系数的关系得![]() ,
,
所以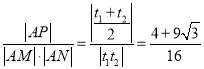 .
.


科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系
轴的正半轴为极轴建立极坐标系![]() ,极坐标系中
,极坐标系中![]() ,弧
,弧![]() 所在圆的圆心分别为
所在圆的圆心分别为![]() ,曲线
,曲线![]() 是弧
是弧![]() ,曲线
,曲线![]() 是弧
是弧![]() ,曲线
,曲线![]() 是弧
是弧![]() ,曲线
,曲线![]() 是弧
是弧![]() .
.
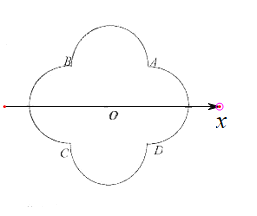
(1)分别写出![]() 的极坐标方程;
的极坐标方程;
(2)直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),点
为参数),点![]() 的直角坐标为
的直角坐标为![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 有两个不同交点
有两个不同交点![]() ,求实数
,求实数![]() 的取值范围,并求出
的取值范围,并求出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),设
为参数),设![]() 与
与![]() 的交点为
的交点为![]() ,当
,当![]() 变化时,
变化时, ![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)写出![]() 的普遍方程及参数方程;
的普遍方程及参数方程;
(2)以坐标原点为极点, ![]() 轴正半轴为极轴建立极坐标系,设曲线
轴正半轴为极轴建立极坐标系,设曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
, ![]() 为曲线
为曲线![]() 上的动点,求点
上的动点,求点![]() 到
到![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年7月1日到3日,世界新能源汽车大会在海南博鳌召开,大会着眼于全球汽车产业的转型升级和生态环境的持续改善.某汽车公司顺应时代潮流,最新研发了一款新能源汽车,并在出厂前对100辆汽车进行了单次最大续航里程(理论上是指新能源汽车所装载的燃料或电池所能够提供给车行驶的最远里程)的测试.现对测试数据进行分析,得到如图的频率分布直方图.

(1)估计这100辆汽车的单次最大续航里程的平均值![]() (同一组中的数据用该组区间的中点值代表);
(同一组中的数据用该组区间的中点值代表);
(2)根据大量的汽车测试数据,可以认为这款汽车的单次最大续航量程X近似地服从正态分布![]() ,经计算第(1)问中样本标准差s的近似值为50.用样本平均数
,经计算第(1)问中样本标准差s的近似值为50.用样本平均数![]() 作为
作为![]() 的近似值,用样本标准差s作为
的近似值,用样本标准差s作为![]() 的估计值,现任取一辆汽车,求它的单次最大续航里程恰在250千米到400千米之间的概率;
的估计值,现任取一辆汽车,求它的单次最大续航里程恰在250千米到400千米之间的概率;
(3)某汽车销售公司为推广此款新能源汽车,现面向意向客户推出“玩游戏,送大奖”活动,客户可根据抛掷硬币的结果,操控微型遥控车在方格图上行进,若遥控车最终停在“胜利大本营”,则可获得购车优惠券.已知硬币出现正,反面的概率都是![]() ,方格图上标有第0格、第1格、第2格……第50格.遥控车开始在第0格,客户每掷一次硬币,遥控车向前移动一次,若掷出正面,遥控车向前移动一格(从k到
,方格图上标有第0格、第1格、第2格……第50格.遥控车开始在第0格,客户每掷一次硬币,遥控车向前移动一次,若掷出正面,遥控车向前移动一格(从k到![]() ),若掷出反面,遥控车向前移动两格(从k到
),若掷出反面,遥控车向前移动两格(从k到![]() ),直到遥控车移到第49格(胜利大本营)或第50格(失败大本营)时,游戏结束.设遥控车移到第n格的概率为
),直到遥控车移到第49格(胜利大本营)或第50格(失败大本营)时,游戏结束.设遥控车移到第n格的概率为![]() ,试证明
,试证明![]() 是等比数列,并解释此方案能否成功吸引顾客购买该款新能源汽车.
是等比数列,并解释此方案能否成功吸引顾客购买该款新能源汽车.
参考数据:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
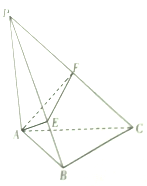
【题目】《九章算术》中,将四个面都为直角三角形的四面体称为鳖臑,如图,在鳖臑![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,且
,且![]() ,过
,过![]() 点分别作
点分别作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,连接
,连接![]() ,则三棱锥
,则三棱锥![]() 的体积的最大值为__________.
的体积的最大值为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为抗击新型冠状病毒,普及防护知识,某校开展了“疫情防护”网络知识竞赛活动.现从参加该活动的学生中随机抽取了100名学生,将他们的比赛成绩(满分为100分)分为6组:![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.
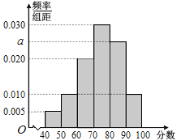
(1)求![]() 的值,并估计这100名学生的平均成绩(同一组中的数据用该组区间的中点值为代表);
的值,并估计这100名学生的平均成绩(同一组中的数据用该组区间的中点值为代表);
(2)在抽取的100名学生中,规定:比赛成绩不低于80分为“优秀”,比赛成绩低于80分为“非优秀”.请将下面的2×2列联表补充完整,并判断是否有99%的把握认为“比赛成绩是否优秀与性别有关”?
优秀 | 非优秀 | 合计 | |
男生 | 40 | ||
女生 | 50 | ||
合计 | 100 |
参考公式及数据:![]() .
.
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子中有大小、形状完全相同的四个小球,分别写有“和”、“谐”、“校”、“园”四个字,有放回地从中任意摸出一个小球,直到“和”、“谐”两个字都摸到就停止摸球,用随机模拟的方法估计恰好在第三次停止摸球的概率。利用电脑随机产生![]() 到
到![]() 之间取整数值的随机数,分别用
之间取整数值的随机数,分别用![]() ,
,![]() ,
,![]() ,
,![]() 代表“和”、“谐”、“校”、“园”这四个字,以每三个随机数为一组,表示摸球三次的结果,经随机模拟产生了以下
代表“和”、“谐”、“校”、“园”这四个字,以每三个随机数为一组,表示摸球三次的结果,经随机模拟产生了以下![]() 组随机数:
组随机数:
![]()
由此可以估计,恰好第三次就停止摸球的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校学生社团组织活动丰富,学生会为了解同学对社团活动的满意程度,随机选取了100位同学进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照[40,50),[50,60),[60,70),…,[90,100]分成6组,制成如图所示频率分布直方图.
(1)求图中x的值;
(2)求这组数据的中位数;
(3)现从被调查的问卷满意度评分值在[60,80)的学生中按分层抽样的方法抽取5人进行座谈了解,再从这5人中随机抽取2人作主题发言,求抽取的2人恰在同一组的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com