
【题目】(14分)一根直木棍长为6m,现将其锯为2段.
(1)若两段木棍的长度均为正整数,求恰有一段长度为2m的概率;
(2)求锯成的两段木棍的长度均大于2m的概率.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)利用列举法求出所有事件共有5种,其中恰有一段长度为2m的情况共计2种,利用古典概型公式可得结果;(2)锯成的两段木棍的长度均大于![]() 的锯点是中间
的锯点是中间![]() 的线段由于木棍总长为6m,由几何概型概率公式可得结果.
的线段由于木棍总长为6m,由几何概型概率公式可得结果.
试题解析:(1)∵两段木棍的长度均为正整数,
∴两段木棍的长度分别为1m和5m,2m和4m,3m和3m,4m和2m,5m和1m,共计5种可能的情况,…(2分)
其中恰有一段长度为2m的情况共计2种,
记“若两段木棍的长度均为正整数,恰有一段长度为2m”为事件A,
∴![]() ,
,
答:若两段木棍的长度均为正整数,恰有一段长度为2m的概率为![]() .
.
(2)记“锯成的两段木棍的长度均大于2m”为事件B,
∴![]() ,
,
答:锯成的两段木棍的长度均大于2m的概率为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知直线![]() ,若存在实数
,若存在实数![]() 使得一条曲线与直线
使得一条曲线与直线![]() 由两个不同的交点,且以这两个交点为端点的线段长度恰好等于
由两个不同的交点,且以这两个交点为端点的线段长度恰好等于![]() ,则称此曲线为直线
,则称此曲线为直线![]() 的“绝对曲线”.下面给出的四条曲线方程:
的“绝对曲线”.下面给出的四条曲线方程:
①![]() ;②
;② ![]() ;③
;③![]() ;④
;④![]() .
.
其中直线![]() 的“绝对曲线”的条数为( )
的“绝对曲线”的条数为( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某折叠餐桌的使用步骤如图所示,有如图检查项目:
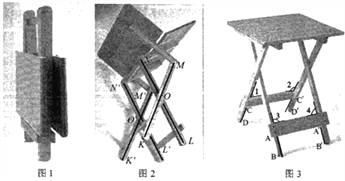
项目①:折叠状态下(如图1),检查四条桌腿长相等;
项目②:打开过程中(如图2),检查![]() ;
;
项目③:打开过程中(如图2),检查![]() ;
;
项目④:打开后(如图3),检查![]() ;
;
项目⑤:打开后(如图3),检查![]() .
.
在检查项目的组合中,可以正确判断“桌子打开之后桌面与地面平行的是”( )
A. ①②③ B. ②③④ C. ②④⑤ D. ③④⑤
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(14分)关于x的不等式ax2+(a﹣2)x﹣2≥0(a∈R)
(1)已知不等式的解集为(﹣∞,﹣1]∪[2,+∞),求a的值;
(2)解关于x的不等式ax2+(a﹣2)x﹣2≥0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一户居民根据以往的月用电量情况,绘制了月用电量的频率分布直方图(月用电量都在25度到325度之间)如图所示.将月用电量落入该区间的频率作为概率.若每月的用电量在200度以内(含200度),则每度电价0.5元,若每月的用电量超过200度,则超过的部分每度电价0.6元.记![]() (单位:度,
(单位:度,![]() )为该用户下个月的用电量,
)为该用户下个月的用电量,![]() (单位:元)为下个月所缴纳的电费.
(单位:元)为下个月所缴纳的电费.
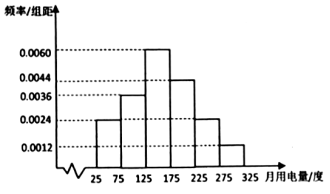
(1)估计该用户的月用电量的平均值(同一组中的数据用该组区间的中点值作代表);
(2)将![]() 表示为
表示为![]() 的函数;
的函数;
(3)根据直方图估计下个月所缴纳的电费![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】是否存在一个等比数列{an}同时满足下列三个条件:①a1+a6=11且a3a4= ![]() ;②an+1>an(n∈N*);③至少存在一个m(m∈N*且m>4),使得
;②an+1>an(n∈N*);③至少存在一个m(m∈N*且m>4),使得 ![]() am﹣1 , am2 , am+1+
am﹣1 , am2 , am+1+ ![]() 依次构成等差数列?若存在,求出通项公式;若不存在,说明理由.
依次构成等差数列?若存在,求出通项公式;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
, ![]() (
(![]() ).
).
(1)求函数![]() 的单调增区间;
的单调增区间;
(2)当![]() 时,记
时,记![]() ,是否存在整数
,是否存在整数![]() ,使得关于
,使得关于![]() 的不等式
的不等式![]() 有解?若存在,请求出
有解?若存在,请求出![]() 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com