
【题目】已知函数![]() ,
,![]() ,
,![]() 为自然对数的底数.
为自然对数的底数.
(Ⅰ)若![]() 为单调递增函数,求实数
为单调递增函数,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)当![]() 存在极小值时,设极小值点为
存在极小值时,设极小值点为![]() ,求证:
,求证:![]() .
.
【答案】(Ⅰ)![]() (Ⅱ)见解析
(Ⅱ)见解析
【解析】
(Ⅰ)由![]() ,可令
,可令![]() ,然后,
,然后,![]() ,然后通过讨论
,然后通过讨论![]() 的单调性,进而可以求出
的单调性,进而可以求出![]() 的最小值,又由
的最小值,又由![]() 为单调递增函数,即可求解.
为单调递增函数,即可求解.
(Ⅱ)利用导数的方法可得出,当![]() 时,
时,![]() ①,利用
①,利用![]() ,得
,得![]() ②,然后,利用①和②可得,
②,然后,利用①和②可得,![]() ,进而令函数
,进而令函数![]() ,利用
,利用![]() 的单调性,即可求证
的单调性,即可求证![]() .
.
解:(Ⅰ)由题意知![]() ,
,
由![]() 为增函数可知
为增函数可知![]() 恒成立.
恒成立.
设![]() ,
,![]() ,
,
令![]() 得
得![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调递减,即
单调递减,即![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,
,![]() 单调递增,即
单调递增,即![]() 单调递增.
单调递增.
故![]() ,又由
,又由![]() 为单调递增函数,则
为单调递增函数,则![]() 恒成立,因此,
恒成立,因此,![]() ,所以,
,所以,![]() .
.
经检验,当![]() 时,满足题意.
时,满足题意.
(Ⅱ)由(Ⅰ)知![]() 时,
时,![]() .
.
又因为![]() ,
,![]() ,且
,且![]() 在
在![]() 上单调递减,
上单调递减,
所以存在![]() 使得
使得![]() ,
,![]() ,
,
令![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
故![]() ,
,
又![]() ,
,![]() 在
在![]() 上单调递增,故存在
上单调递增,故存在![]() 使得
使得![]() .
.
因此有![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
故![]() ,
,![]() ,利用
,利用![]()
将![]() 代入消去
代入消去![]() 得
得![]() ,
,
函数![]() 的对称轴为
的对称轴为![]() ,
,
故![]() 在
在![]() 上单调递减,
上单调递减,
因此![]() ,即
,即![]() 成立.
成立.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知曲线C的参数方程为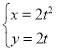 (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为ρ(
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为ρ(![]() cosθ+sinθ)=8.
cosθ+sinθ)=8.
(1)求曲线C和直线l的直角坐标方程;
(2)若射线m的极坐标方程为θ![]() (ρ≥0),设m与C相交于点M(非坐标原点),m与l相交于点N,点P(6,0),求△PMN的面积.
(ρ≥0),设m与C相交于点M(非坐标原点),m与l相交于点N,点P(6,0),求△PMN的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了积极稳妥疫情期间的复学工作,市教育局抽调5名机关工作人员去某街道3所不同的学校开展驻点服务,每个学校至少去1人,若甲、乙两人不能去同一所学校,则不同的分配方法种数为___________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以平面直角坐标系![]() 的原点
的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,取相同的单位长度建立极坐标系,直线
轴的正半轴为极轴,取相同的单位长度建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为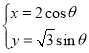 (
(![]() 为参数).
为参数).
(Ⅰ)求直线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的普通方程;
的普通方程;
(Ⅱ)求曲线![]() 上的动点到直线
上的动点到直线![]() 距离的最大值.
距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 和圆
和圆![]() :
:![]() ,
,![]() ,
,![]() 为椭圆
为椭圆![]() 的左、右焦点,点
的左、右焦点,点![]() 在椭圆
在椭圆![]() 上,当直线
上,当直线![]() 与圆
与圆![]() 相切时,
相切时,![]() .
.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)直线![]() :
:![]() 与
与![]() 轴交于点
轴交于点![]() ,且与椭圆
,且与椭圆![]() 和圆
和圆![]() 都相切,切点分别为
都相切,切点分别为![]() ,
,![]() ,记
,记![]() 和
和![]() 的积分别为
的积分别为![]() 和
和![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为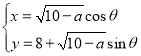 (
(![]() 为参数,常数
为参数,常数![]() ).以坐标原点为极点,
).以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,已知直线
轴的正半轴为极轴建立极坐标系,已知直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出![]() 及直线
及直线![]() 的直角坐标方程,并指出
的直角坐标方程,并指出![]() 是什么曲线;
是什么曲线;
(2)设![]() 是曲线
是曲线![]() 上的一个动点,求点
上的一个动点,求点![]() 到直线
到直线![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com