[题目]已知函数f(x)的图象在点(x0 . f(x0))处的切线方程l:y=g满足x∈I的定义域).当x≠x0时.[f](x﹣x0)＞0恒成立.则称x0为函数f(x)的“穿越点．已知函数f(x)=lnx﹣ x2﹣ 在(0.e]上存在一个“穿越点 .则a的取值范围为( )A.[ .+∞)??B.(﹣1. ]??C.[﹣ .1)??D.(﹣∞.﹣ ] 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】已知函数f（x）的图象在点（x0 ， f（x0））处的切线方程l：y=g（x），若函数f（x）满足x∈I（其中I为函数f（x）的定义域），当x≠x0时，[f（x）﹣g（x）]（x﹣x0）＞0恒成立，则称x0为函数f（x）的“穿越点”．已知函数f（x）=lnx﹣ x2﹣ 在（0，e]上存在一个“穿越点”，则a的取值范围为（）
A.[ ，+∞）??
B.（﹣1， ]??
C.[﹣ ，1）??
D.（﹣∞，﹣ ]

【答案】D
【解析】解：根据若函数f（x）满足x∈I（其中I为函数f（x）的定义域），当x≠x0时，[f（x）﹣g（x）]（x﹣x0）＞0恒成立，利用二阶导函数为0，求解：f″（x）=﹣ ﹣a=0，显然只有当a＜0时有解，其解就为“穿越点”横坐标，
故x= ，由题意x= ∈（0，e]，故a≤﹣ ．
故选：D

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】如图（1）所示，在直角梯形ABCD中，，E是AD的中点，O是AC与BE的交点．将△ABE沿BE折起到△A1BE的位置，如图（2）所示．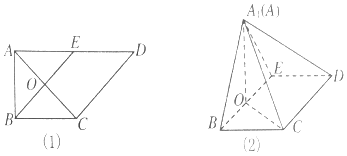
（1）证明：CD⊥平面A1OC；
（2）若平面A1BE⊥平面BCDE，求平面A1BC与平面A1CD所成锐二面角的余弦值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】若a1=1，对任意的n∈N* ，都有an＞0，且nan+12﹣（2n﹣1）an+1an﹣2an2=0设M（x）表示整数x的个位数字，则M（a2017）= ．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】设函数f（x）=|x﹣2|+2x﹣3，记f（x）≤﹣1的解集为M．
（Ⅰ）求M；
（Ⅱ）当x∈M时，证明：x[f（x）]2﹣x2f（x）≤0．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】设数列的前n项和为Sn ，且满足：
① ；② ，其中且．
（1）求p的值；
（2）数列能否是等比数列？请说明理由；
（3）求证：当r 2时，数列是等差数列．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图1，四边形ABCD为直角梯形，AD∥BC，AD⊥AB，AD=1，BC=2，E为CD上一点，F为BE的中点，且DE=1，EC=2，现将梯形沿BE折叠（如图2），使平面BCE⊥ABED．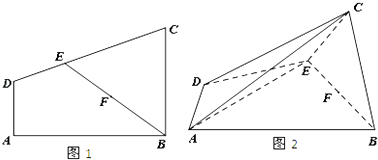

（1）求证：平面ACE⊥平面BCE；
（2）能否在边AB上找到一点P（端点除外）使平面ACE与平面PCF所成角的余弦值为？若存在，试确定点P的位置，若不存在，请说明理由．