
【题目】已知![]() ,直线
,直线![]() 与曲线
与曲线![]() 相切,设
相切,设![]() 的最大值为
的最大值为![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() ,则( )
,则( )
A.存在![]() ,
,![]()
B.![]() 为等差数列
为等差数列
C.对于![]() ,
,![]()
D.![]()
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,左、右焦点分别为
,左、右焦点分别为![]() 、
、![]() ,抛物线
,抛物线![]() 的焦点
的焦点![]() 恰好是该椭圆的一个顶点.
恰好是该椭圆的一个顶点.
(1)求椭圆![]() 的方程;
的方程;
(2)已知圆![]() 的切线
的切线![]() (直线
(直线![]() 的斜率存在且不为零)与椭圆相交于
的斜率存在且不为零)与椭圆相交于![]() 、
、![]() 两点,那么以
两点,那么以![]() 为直径的圆是否经过定点?如果是,求出定点的坐标;如果不是,请说明理由.
为直径的圆是否经过定点?如果是,求出定点的坐标;如果不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行双12有奖促销活动,顾客购买168元的商品后即可抽奖,抽奖方法是:从装有2个红球![]() 和1个白球
和1个白球![]() 的甲箱与装有2个红球
的甲箱与装有2个红球![]() 和1个白球
和1个白球![]() 的乙箱中,各随机摸出1个球,这些球除颜色,标号外都一样.若摸出的2个球颜色相同则中奖,否则不中奖.
的乙箱中,各随机摸出1个球,这些球除颜色,标号外都一样.若摸出的2个球颜色相同则中奖,否则不中奖.
(1)用球的标号列出所有可能的摸出结果;
(2)小明根据经验认为:摸到同色球一般来说更为难得,所以猜测中奖的概率小于不中奖的概率,你认为小明的猜想正确吗?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() 为常数.
为常数.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)已知![]() 是以2为周期的偶函数,且当
是以2为周期的偶函数,且当![]() 时,有
时,有![]() .若
.若![]() ,且
,且![]() ,求函数
,求函数![]()
![]() 的反函数;
的反函数;
(3)若在![]() 上存在
上存在![]() 个不同的点
个不同的点![]() ,
,![]() ,使得
,使得![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】今天你低碳了吗?近来国内网站流行一种名为“碳排放计算器”的软件,人们可以由此计算出自己每天的碳排放量,如家居用电的碳排放量(千克)=耗电度数×0.785,汽车的碳排放量(千克)=油耗公升数×0.785等,某班同学利用寒假在两个小区逐户进行了一次生活习惯是否符合低碳观念的调查.若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,这二族人数占各自小区总人数的比例P数据如下:
A小区 | 低碳族 | 非低碳族 | B小区 | 低碳族 | 非低碳族 | |
比例P | 1/2 | 1/2 | 比例P | 4/5 | 1/5 |
(1)如果甲、乙来自A小区,丙、丁来自B小区,求这4人中恰好有两人是低碳族的概率;
(2)A小区经过大力宣传,每周非低碳中有20%的人加入到低碳族的行列,如果两周后随机地从A小区中任选25个人,记![]() 表示25个人中的低碳族人数,求E
表示25个人中的低碳族人数,求E![]() 和
和![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解高三男生的体能达标情况,抽调了120名男生进行立定跳远测试,根据统计数据得到如下的频率分布直方图.若立定跳远成绩落在区间![]() 的左侧,则认为该学生属“体能不达标的学生,其中
的左侧,则认为该学生属“体能不达标的学生,其中![]() 分别为样本平均数和样本标准差,计算可得
分别为样本平均数和样本标准差,计算可得![]() (同一组中的数据用该组区间的中点值作代表).
(同一组中的数据用该组区间的中点值作代表).
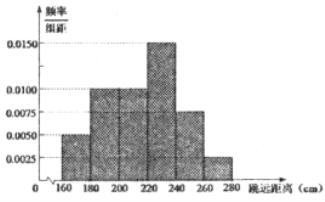
(1)若该校高三某男生的跳远距离为![]() ,试判断该男生是否属于“体能不达标”的学生?
,试判断该男生是否属于“体能不达标”的学生?
(2)该校利用分层抽样的方法从样本区间![]() 中共抽出5人,再从中选出两人进行某体能训练,求选出的两人中恰有一人跳远距离在
中共抽出5人,再从中选出两人进行某体能训练,求选出的两人中恰有一人跳远距离在![]() 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com