
【题目】已知实数x,y满足 ,则
,则![]() 的最大值为________,
的最大值为________,![]() 的最小值为________.
的最小值为________.
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是平行四边形,
是平行四边形,![]() ,侧面
,侧面![]() 底面
底面![]() ,
,![]() ,
,![]() ,
, ![]() 分别为
分别为![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上.
上.
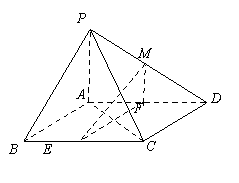
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)如果直线![]() 与平面
与平面![]() 所成的角和直线
所成的角和直线![]() 与平面
与平面![]() 所成的角相等,求
所成的角相等,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“一带一路”是“丝绸之路经济带”和“21世纪海上丝绸之路”的简称.某市为了了解人们对“一带一路”的认知程度,对不同年龄和不同职业的人举办了一次“一带一路”知识竞赛,满分100分(90分及以上为认知程度高).现从参赛者中抽取了![]() 人,按年龄分成5组,第一组:
人,按年龄分成5组,第一组: ![]() ,第二组:
,第二组: ![]() ,第三组:
,第三组: ![]() ,第四组:
,第四组: ![]() ,第五组:
,第五组: ![]() ,得到如图所示的频率分布直方图,已知第一组有6人.
,得到如图所示的频率分布直方图,已知第一组有6人.
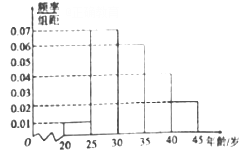
(1)求![]() ;
;
(2)求抽取的![]() 人的年龄的中位数(结果保留整数);
人的年龄的中位数(结果保留整数);
(3)从该市大学生、军人、医务人员、工人、个体户 五种人中用分层抽样的方法依次抽取6人,42人,36人,24人,12人,分别记为1~5组,从这5个按年龄分的组和5个按职业分的组中每组各选派1人参加知识竞赛,分别代表相应组的成绩,年龄组中1~5组的成绩分别为93,96,97,94,90,职业组中1~5组的成绩分别为93,98,94,95,90.
(Ⅰ)分别求5个年龄组和5个职业组成绩的平均数和方差;
(Ⅱ)以上述数据为依据,评价5个年龄组和5个职业组对“一带一路”的认知程度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】总体由编号为![]() 的20个个体组成,利用下面的随机数表选取6个个体,选取方法是从随机数表第一行的第5列和第6列数字开始由左到右依次选取两个数字,则选出来的第6个个体的编号为( )
的20个个体组成,利用下面的随机数表选取6个个体,选取方法是从随机数表第一行的第5列和第6列数字开始由左到右依次选取两个数字,则选出来的第6个个体的编号为( )
7816 | 6572 | 0802 | 6314 | 0702 | 4369 | 1128 | 0598 |
3204 | 9234 | 4935 | 8200 | 3623 | 4869 | 6938 | 7481 |
A.08B.07C.02D.05
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年某市有2万多文科考生参加高考,除去成绩为![]() 分(含
分(含![]() 分)以上的3人与成绩为
分)以上的3人与成绩为![]() 分(不含
分(不含![]() 分)以下的3836人,还有约1.9万文科考生的成绩集中在
分)以下的3836人,还有约1.9万文科考生的成绩集中在![]() 内,其成绩的频率分布如下表所示:
内,其成绩的频率分布如下表所示:
分数段 |
|
|
|
|
频率 | 0.108 | 0.133 | 0.161 | 0.183 |
分数段 |
|
|
|
|
频率 | 0.193 | 0.154 | 0.061 | 0.007 |
(Ⅰ)试估计该次高考成绩在![]() 内文科考生的平均分(精确到
内文科考生的平均分(精确到![]() );
);
(Ⅱ)一考生填报志愿后,得知另外有4名同分数考生也填报了该志愿.若该志愿计划录取3人,并在同分数考生中随机录取,求该考生不被该志愿录取的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com