
【题目】如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧远处一山顶D在西偏北![]() 的方向上,仰角为
的方向上,仰角为![]() ,行驶4km后到达B处,测得此山顶在西偏北
,行驶4km后到达B处,测得此山顶在西偏北![]() 的方向上.
的方向上.
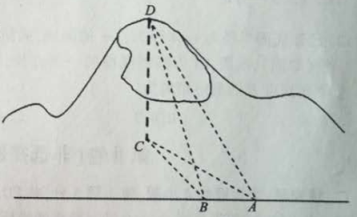
(1)求此山的高度(单位:km);
(2)设汽车行驶过程中仰望山顶D的最大仰角为![]() ,求
,求![]() .
.
 目标测试系列答案
目标测试系列答案科目:高中数学 来源: 题型:
【题目】如图,四面体ABCD中,O是BD的中点,CA=CB=CD=BD=2,AB=AD=![]() .
.
(1)求证:AO⊥平面BCD;
(2)求异面直线AB与CD所成角的大小;
(3)求二面角O﹣AC﹣D的大小.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一年级新入学360名学生,其中200名男生,160名女生.学校计划为家远的高一新生提供5间男生宿舍和4间女生宿舍,每间宿舍可住2名学生.该校“数学与统计”社团的学生为了解全体高一学生家庭居住地与学校的距离情况,按照性别进行分层随机抽样,其中抽取的40名男生家庭居住地与学校的距离数据(单位:![]() )如下:
)如下:
5.0 | 6.0 | 7.0 | 7.5 | 8.0 | 8.4 | 4.0 | 3.5 | 4.5 |
4.3 | 5.0 | 4.0 | 3.0 | 2.5 | 4.0 | 1.6 | 6.0 | 6.5 |
5.5 | 5.7 | 3.1 | 5.2 | 4.4 | 5.0 | 6.4 | 3.5 | 7.0 |
4.0 | 3.0 | 3.4 | 6.9 | 4.8 | 5.6 | 5.0 | 5.6 | 6.5 |
3.0 | 6.0 | 7.0 | 6.6 |
(1)根据以上样本数据推断,若男生甲家庭居中地与学校距离为![]() ,他是否能住宿?说明理由;
,他是否能住宿?说明理由;
(2)通过计算得到男生样本数据平均值为![]() ,女生样本数据平均值为
,女生样本数据平均值为![]() ,求所有样本数据的平均值.
,求所有样本数据的平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数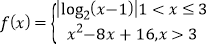 若方程f(x)=m有4个不同的实根x1,x2,x3,x4,且x1<x2<x3<x4,则(
若方程f(x)=m有4个不同的实根x1,x2,x3,x4,且x1<x2<x3<x4,则(![]() )(x3+x4)=( )
)(x3+x4)=( )
A. 6 B. 7 C. 8 D. 9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在去年的足球甲![]() 联赛上,一队每场比赛平均失球数是1.5,全年比赛失球个数的标准差为1.1;二队每场比赛平均失球数是2.1,全年失球个数的标准差是0.4,你认为下列说法中正确的个数有( )
联赛上,一队每场比赛平均失球数是1.5,全年比赛失球个数的标准差为1.1;二队每场比赛平均失球数是2.1,全年失球个数的标准差是0.4,你认为下列说法中正确的个数有( )
①平均来说一队比二队防守技术好;②二队比一队防守技术水平更稳定;③一队防守有时表现很差,有时表现又非常好;④二队很少不失球.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是公差为2的等差数列,数列{bn}满足b1=1,b2=2,且anbn+bn=nbn+1(bn≠0).
(1)求数列{an},{bn}的通项公式;
(2)设cn=![]() ,求数列{cn}的前n项和Sn.
,求数列{cn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于平面上任意![]() 个点构成的点集
个点构成的点集![]() ,如果其中任意两点之间的距离均已确定,那么就称这个点集是“稳定的”.求证:在
,如果其中任意两点之间的距离均已确定,那么就称这个点集是“稳定的”.求证:在![]() 格点的平面点集
格点的平面点集![]() 中,无三点共线,且其中的
中,无三点共线,且其中的![]() 个两点之间的距离已被确定,那么点集
个两点之间的距离已被确定,那么点集![]() 就是“稳定的”.
就是“稳定的”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的参数方程为
的参数方程为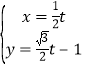 (
(![]() 为参数).在以坐标原点
为参数).在以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,且与直角坐标系长度单位相同的极坐标系中,曲线
轴的正半轴为极轴,且与直角坐标系长度单位相同的极坐标系中,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() .若直
.若直![]() 与曲线
与曲线![]() 相交于两点
相交于两点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线![]() 的参数方程为
的参数方程为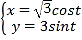 (t为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程是
(t为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程是![]() ,曲线
,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)求直线l和曲线![]() 的直角坐标方程,曲线
的直角坐标方程,曲线![]() 的普通方程;
的普通方程;
(2)若直线l与曲线![]() 和曲线
和曲线![]() 在第一象限的交点分别为P,Q,求
在第一象限的交点分别为P,Q,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com