
| x2 |
| 25 |
| y2 |
| 9 |
| x2 |
| 35 |
| x2 |
| 25 |
| y2 |
| 9 |
| x2 |
| 35 |
| 34 |
| 1 |
| 2 |
| 1 |
| 2 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| 25 |
| y2 |
| 9 |
| x2 |
| 35 |
查看答案和解析>>
科目:高中数学 来源:浙江省富阳市第二中学2008-2009学年高二第二学期3月月考理科数学试题 题型:013
以下四个命题中,正确的是
A.若![]() ,则P、A、B三点共线
,则P、A、B三点共线
B.△ABC是直角三角形的充要条件是![]()
C.设向量![]() 是空间一个基底,则{
是空间一个基底,则{![]() +
+![]() ,
,![]() +
+![]() ,
,![]() +
+![]() }构成空间的另一个基底
}构成空间的另一个基底
D.|(![]() ·
·![]() )
)![]() |=|
|=|![]() |·|
|·|![]() |·|
|·|![]() |
|
查看答案和解析>>
科目:高中数学 来源:2013届浙江省高二下学期期中考试文科数学试卷(解析版) 题型:选择题
用反证法证明命题:“一个三角形中不能有两个直角”的过程归纳为以下三个步骤:
①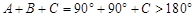 ,这与三角形内角和为
,这与三角形内角和为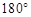 相矛盾,
相矛盾,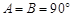 不成立
不成立
②所以一个三角形中不能有两个直角;③假设三角形的三个内角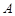 、
、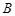 、
、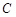 中有两个直角,
中有两个直角,
不妨设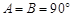 .正确顺序的序号为( )
.正确顺序的序号为( )
A.①②③ B.③②① C.②③① D.③①②
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com