
【题目】(1)在等差数列![]() 中,已知
中,已知![]() ,前
,前![]() 项和为
项和为![]() ,且
,且![]() ,求当
,求当![]() 取何值时,
取何值时, ![]() 取得最大值,并求出它的最大值;
取得最大值,并求出它的最大值;
(2)已知数列![]() 的通项公式是
的通项公式是![]() ,求数列
,求数列![]() 的前
的前![]() 项和.
项和.
【答案】(1)当![]() 或
或![]() 时,
时, ![]() 取得最大值为
取得最大值为![]() (2)
(2)![]()
【解析】试题分析:(1)由已知得![]() ,从而
,从而![]() ,进而求出
,进而求出![]() ,根据二次函数的性质可得当
,根据二次函数的性质可得当![]() 或
或![]() 时,
时, ![]() 取得最大值
取得最大值![]() ;(2)由已知得
;(2)由已知得![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列,从而数列
的等差数列,从而数列![]() 的前
的前![]() 项和
项和![]() ,由
,由![]() ,得
,得![]() ,从而
,从而![]() 时,
时, ![]() 时,
时, ![]() ,由此能求出数列
,由此能求出数列![]() 的前
的前![]() 项和.
项和.
试题解析: (1)方法一 ∵a1=20,S10=S15,
∴10×20+![]() d=15×20+
d=15×20+![]() d,∴d=-
d,∴d=-![]() .
.
∴an=20+(n-1)×![]() =-
=-![]() n+
n+![]() .
.
∴a13=0,即当n≤12时,an>0,n≥14时,an<0,
∴当n=12或13时,Sn取得最大值,且最大值为S13=S12=12×20+![]() =130.
=130.
(2)∵an=4n-25,an+1=4(n+1)-25,∴an+1-an=4=d,又a1=4×1-25=-21.
所以数列{an}是以-21为首项,以4为公差的递增的等差数列.
令 ,由①得n<6
,由①得n<6![]() ;由②得n≥5
;由②得n≥5![]() ,所以n=6.
,所以n=6.
即数列{|an|}的前6项是以21为首项,公差为-4的等差数列,从第7项起以后各项构成公差为4的等差数列,
而|a7|=a7=4×7-25=3.设{|an|}的前n项和为Tn,则
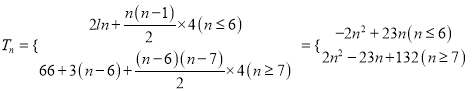


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源: 题型:
【题目】在极坐标系中,圆![]() 的极坐标方程为
的极坐标方程为![]() ,若以极点
,若以极点![]() 为原点,极轴所在的直线为
为原点,极轴所在的直线为![]() 轴建立平面直角坐标系.
轴建立平面直角坐标系.
(1)求圆![]() 的参数方程;
的参数方程;
(2)在直线坐标系中,点![]() 是圆
是圆![]() 上的动点,试求
上的动点,试求![]() 的最大值,并求出此时点
的最大值,并求出此时点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】求椭圆的标准方程
(1)已知某椭圆的左右焦点分别为F1(﹣1,0),F2(1,0),且经过点P( ![]() ,
, ![]() ),求该椭圆的标准方程;
),求该椭圆的标准方程;
(2)已知某椭圆过点( ![]() ,﹣1),(﹣1,
,﹣1),(﹣1, ![]() ),求该椭圆的标准方程.
),求该椭圆的标准方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学生在一门功课的22次考试中,所得分数茎叶图如图所示,则此学生该门功课考试分数的极差与中位数之和为( ) 
A.117
B.118
C.118.5
D.119.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年6月22 日,“国际教育信息化大会”在山东青岛开幕.为了解哪些人更关注“国际教育信息化大会”,某机构随机抽取了年龄在15-75岁之间的100人进行调查,并按年龄绘制成频率分布直方图,如图所示,其分组区间为: ![]() .把年龄落在区间
.把年龄落在区间![]() 和
和![]() 内的人分别称为 “青少年”和“中老年”.
内的人分别称为 “青少年”和“中老年”.
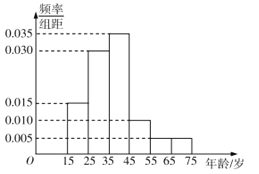
(1)根据频率分布直方图求样本的中位数(保留两位小数)和众数;
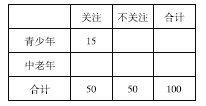
(2)根据已知条件完成下面的![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为“中老年”比“青少年”更加关注“国际教育信息化大会”;
的把握认为“中老年”比“青少年”更加关注“国际教育信息化大会”;
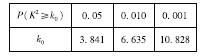
附:参考公式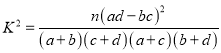 ,其中
,其中![]() .
.
临界值表:
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC满足| ![]() |=3,|
|=3,| ![]() |=4,O是△ABC所在平面内一点,满足|
|=4,O是△ABC所在平面内一点,满足| ![]() |=|
|=| ![]() |=|
|=| ![]() |,且
|,且 ![]() =λ
=λ ![]() +
+ ![]()
![]() (λ∈R),则cos∠BAC= .
(λ∈R),则cos∠BAC= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对同一类的![]() ,
,![]() ,
,![]() ,
,![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”;
作品获得一等奖”;
乙说:“![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“![]() ,
,![]() 两项作品未获得一等奖”;
两项作品未获得一等奖”;
丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com