
【题目】已知函数f(x)=xlnx﹣x+1,g(x)=ex﹣ax,a∈R.
(Ⅰ)求f(x)的最小值;
(Ⅱ)若g(x)≥1在R上恒成立,求a的值;
(Ⅲ)求证:![]() .
.
【答案】(Ⅰ)0(Ⅱ)a=1;(III)见解析
【解析】
(I)对f(x)求导,分析导函数的正负,得到函数f(x)的单调性,即得解.
(Ⅱ)由g(x)=ex﹣ax≥1恒成立可得ax+1≤ex恒成立,可求得函数y=h(x)在(0,1)处的切线方程为y=x+1,故可得证.
(III)由(Ⅱ)两边取对数得ln(x+1)≤x,令x![]() ,可得证.
,可得证.
(I)f'(x)=lnx,
∴当0<x<1时,f'(x)<0,x>1时,f'(x)>0,
∴f(x)在(0,1)上单调递减,在(1,+∞)上单调递增,
∴当x=1时,f(x)取得最小值f(1)=0;
(II)由g(x)=ex﹣ax≥1恒成立可得ax+1≤ex恒成立,
设h(x)=ex,则h'(x)=ex,故h'(0)=1,h(0)=1,
∴函数y=h(x)在(0,1)处的切线方程为y=x+1,
∴x+1≤ex恒成立.
∴a=1;
(III)由(II)可知,x+1≤ex恒成立,
两边取对数得ln(x+1)≤x,令x![]() (i=1,2,3…n)累加得
(i=1,2,3…n)累加得
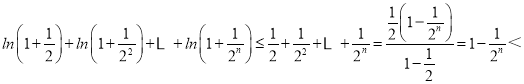 1,
1,
所以原不等式成立.


 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】在全面抗击新冠肺炎疫情这一特殊时期,我市教育局提出“停课不停学”的口号,鼓励学生线上学习.某校数学教师为了调查高三学生数学成绩与线上学习时间之间的相关关系,对高三年级随机选取45名学生进行跟踪问卷,其中每周线上学习数学时间不少于5小时的有19人,余下的人中,在检测考试中数学平均成绩不足120分的占![]() ,统计成绩后得到如下
,统计成绩后得到如下![]() 列联表:
列联表:
分数不少于120分 | 分数不足120分 | 合计 | |
线上学习时间不少于5小时 | 4 | 19 | |
线上学习时间不足5小时 | |||
合计 | 45 |
(1)请完成上面![]() 列联表;并判断是否有99%的把握认为“高三学生的数学成绩与学生线上学习时间有关”;
列联表;并判断是否有99%的把握认为“高三学生的数学成绩与学生线上学习时间有关”;
(2)①按照分层抽样的方法,在上述样本中从分数不少于120分和分数不足120分的两组学生中抽取9名学生,设抽到不足120分且每周线上学习时间不足5小时的人数是![]() ,求
,求![]() 的分布列(概率用组合数算式表示);
的分布列(概率用组合数算式表示);
②若将频率视为概率,从全校高三该次检测数学成绩不少于120分的学生中随机抽取20人,求这些人中每周线上学习时间不少于5小时的人数的期望和方差.
(下面的临界值表供参考)
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式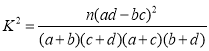 其中
其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知甲盒内有大小相同的1个红球和3个黑球,乙盒内有大小相同的3个红球和3个黑球,现从甲、乙两个盒内各任取2个球。
(1)求取出的4个球中没有红球的概率;
(2)求取出的4个球中恰有1个红球的概率;
(3)设![]() 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求![]() 的分布列和数学期望。
的分布列和数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】追求人类与生存环境的和谐发展是中国特色社会主义生态文明的价值取向.为了改善空气质量,某城市环保局随机抽取了一年内100天的空气质量指数(AQI)的检测数据,结果统计如表:
AQI |
|
|
|
|
|
|
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 重度污染 |
天数 | 6 | 14 | 18 | 27 | 25 | 10 |
(1)从空气质量指数属于[0,50],(50,100]的天数中任取3天,求这3天中空气质量至少有2天为优的概率;
(2)已知某企业每天因空气质量造成的经济损失y(单位:元)与空气质量指数x的关系式为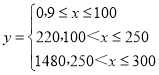 ,假设该企业所在地7月与8月每天空气质量为优、良、轻度污染、中度污染、重度污染、严重污染的概率分别为
,假设该企业所在地7月与8月每天空气质量为优、良、轻度污染、中度污染、重度污染、严重污染的概率分别为![]() .9月每天的空气质量对应的概率以表中100天的空气质量的频率代替.
.9月每天的空气质量对应的概率以表中100天的空气质量的频率代替.
(i)记该企业9月每天因空气质量造成的经济损失为X元,求X的分布列;
(ii)试问该企业7月、8月、9月这三个月因气质量造成的经济损失总额的数学期望是否会超过2.88万元?说明你的理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产甲、乙两种产品均需用![]() 三种原料,一件甲产品需要
三种原料,一件甲产品需要![]() 原料
原料![]() ,
,![]() 原料
原料![]() ,
,![]() 原料
原料![]() ,一件乙产品需要
,一件乙产品需要![]() 原料
原料![]() ,
,![]() 原料
原料![]() ,
,![]() 原料
原料![]() ,出售一件甲产品可获利7万元,出售一件乙产品可获利6万元,现有
,出售一件甲产品可获利7万元,出售一件乙产品可获利6万元,现有![]() 原料
原料![]() ,
,![]() 原料
原料![]() ,
,![]() 原料
原料![]() ,请问该如何安排生产可使得利润最大?
,请问该如何安排生产可使得利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
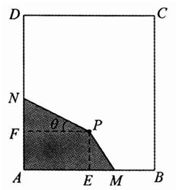
【题目】(题文)如图,长方形材料![]() 中,已知
中,已知![]() ,
,![]() .点
.点![]() 为材料
为材料![]() 内部一点,
内部一点,![]() 于
于![]() ,
,![]() 于
于![]() ,且
,且![]() ,
,![]() . 现要在长方形材料
. 现要在长方形材料![]() 中裁剪出四边形材料
中裁剪出四边形材料![]() ,满足
,满足![]() ,点
,点![]() 、
、![]() 分别在边
分别在边![]() ,
,![]() 上.
上.
(1)设![]() ,试将四边形材料
,试将四边形材料![]() 的面积表示为
的面积表示为![]() 的函数,并指明
的函数,并指明![]() 的取值范围;
的取值范围;
(2)试确定点![]() 在
在![]() 上的位置,使得四边形材料
上的位置,使得四边形材料![]() 的面积
的面积![]() 最小,并求出其最小值.
最小,并求出其最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com