
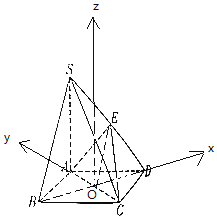
【题目】如图,在四棱锥S﹣ABCD中,SA⊥底面ABCD,底面ABCD是平行四边形,E是线段SD上一点.

(1)若E是SD的中点,求证:SB∥平面ACE;
(2)若SA=AB=AD=2,SC=2![]() ,且DE
,且DE![]() DS,求二面角S﹣AC﹣E的余弦值.
DS,求二面角S﹣AC﹣E的余弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)由题意连结BD,交AC于点O,连结OE,可证OE∥SB,SB∥平面ACE得证;
(2)建立空间直角坐标系,求得平面SAC与平面ACE的法向量,代入公式求二面角的余弦值即可.
(1)证明:连结BD,交AC于点O,连结OE,
∵底面ABCD是平行四边形,∴O是BD的中点,
∵E是SD的中点,∴OE∥SB,
∵SB平面ACE,OE平面ACE,
∴SB∥平面ACE.
(2)∵SA⊥底面ABCD,AC平面ABCD,
∴SA⊥AC,
在Rt△SAC中,SA=2,SC=2![]() ,
,
∴AC=2,
∵AB=AD=2,
∴△ABC,△ACD都是等边三角形,
∴BD=2![]() ,
,
以O为原点,OD为x轴,OA为y轴,过O作AS的平行线为z轴,建立空间直角坐标系,
O(0,0,0),D(![]() ,0,0),A(0,1,0),S(0,1,2),
,0,0),A(0,1,0),S(0,1,2),
![]() (
(![]() ,1,2),
,1,2),![]() (
(![]() ,
,![]() ),
),
![]() (
(![]() ),
),
∵BD⊥平面SAC,取平面SAC的一个法向量![]() (
(![]() ),
),
设平面ACE的法向量![]() (x,y,z),
(x,y,z),
则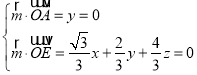 ,取x=4,得
,取x=4,得![]() (4,0,
(4,0,![]() ),
),
设二面角S﹣AC﹣E的平面角为θ,
则cosθ .
.
∴二面角S﹣AC﹣E的余弦值为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
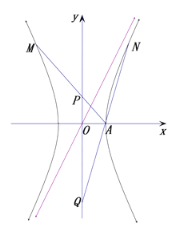
【题目】已知直线![]() 是双曲线
是双曲线![]() 的一条渐近线,点
的一条渐近线,点![]()
![]() 都在双曲线
都在双曲线![]() 上,直线
上,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,设坐标原点为
,设坐标原点为![]() .
.
(1)求双曲线![]() 的方程,并求出点
的方程,并求出点![]() 的坐标(用
的坐标(用![]() 表示);
表示);
(2)设点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,直线
,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() .问:在
.问:在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(3)若过点![]() 的直线
的直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 两点,且
两点,且![]() ,试求直线
,试求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某商场2018年洗衣机、电视机和电冰箱三种电器各季度销量的百分比堆积图(例如:第3季度内,洗衣机销量约占![]() ,电视机销量约占
,电视机销量约占![]() ,电冰箱销量约占
,电冰箱销量约占![]() ).根据该图,以下结论中一定正确的是( )
).根据该图,以下结论中一定正确的是( )
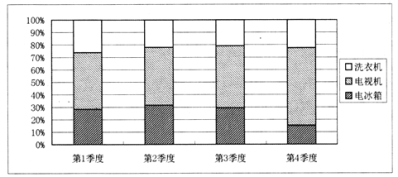
A. 电视机销量最大的是第4季度
B. 电冰箱销量最小的是第4季度
C. 电视机的全年销量最大
D. 电冰箱的全年销量最大
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】按照如下规则构造数表:第一行是:2;第二行是:![]() ;即3,5,第三行是:
;即3,5,第三行是:![]() 即4,6,6,8;
即4,6,6,8;![]() (即从第二行起将上一行的数的每一项各项加1写出,再各项加3写出)
(即从第二行起将上一行的数的每一项各项加1写出,再各项加3写出)
2
3,5
4,6,6,8
5,7,7,9,7,9,9,11
……………………………………
若第![]() 行所有的项的和为
行所有的项的和为![]() .
.
(1)求![]() ;
;
(2)试求![]() 与
与![]() 的递推关系,并据此求出数列
的递推关系,并据此求出数列![]() 的通项公式;
的通项公式;
(3)设![]() ,求
,求![]() 和
和![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 为矩形,
为矩形,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上的动点.
上的动点.
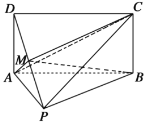
(1)若![]() 为线段
为线段![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(2)若三棱锥![]() 的体积记为
的体积记为![]() ,四棱锥
,四棱锥![]() 的体积记为
的体积记为![]() ,当
,当![]() 时,求二面角
时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 是双曲线
是双曲线![]() 的一条渐近线,点
的一条渐近线,点![]()
![]() 都在双曲线
都在双曲线![]() 上,直线
上,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,设坐标原点为
,设坐标原点为![]() .
.
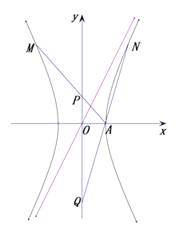
(1)求双曲线![]() 的方程,并求出点
的方程,并求出点![]() 的坐标(用
的坐标(用![]() 表示);
表示);
(2)设点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,直线
,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() .问:在
.问:在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(3)若过点![]() 的直线
的直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 两点,且
两点,且![]() ,试求直线
,试求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com