
【题目】如图,已知抛物线x2=y,点![]() ,抛物线上的点
,抛物线上的点![]() ,过点B作直线AP的垂线,垂足为Q.
,过点B作直线AP的垂线,垂足为Q.
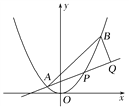
(1)求直线AP斜率的取值范围;
(2)求|PA|·|PQ|的最大值.
【答案】(1)(-1,1).(2) ![]() .
.
【解析】试题分析:
(1)通过点![]() 在抛物线上,可设
在抛物线上,可设![]() ,利用斜率公式结合
,利用斜率公式结合![]() 可得结论;
可得结论;
(2)通过(1)值![]() ,
, ![]() ,设直线
,设直线![]() 的斜率为
的斜率为![]() ,联立直线
,联立直线![]() 方程可知
方程可知![]() 点坐标,进而可用
点坐标,进而可用![]() 表示
表示![]() ,计算
,计算![]() ,通过令
,通过令![]() ,求导结合单调性可得结论.
,求导结合单调性可得结论.
试题解析:
(1)由题意得P(x,x2),-![]() <x<
<x<![]() .
.
设直线AP的斜率为k,
故k=![]() =x-
=x-![]() ∈(-1,1),
∈(-1,1),
故直线AP斜率的取值范围为(-1,1).
(2)由(1)知P![]() ,-
,-![]() <x<
<x<![]() ,
,
则直线AP的方程为:y=kx+![]() k+
k+![]() ,
,
直线BQ的方程为:y=-![]() x+
x+![]() +
+![]() ,
,
联立直线AP与BQ的方程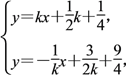 解得点Q的横坐标是xQ=
解得点Q的横坐标是xQ=![]() ,
,
因为|PA|=![]()
![]() =
=![]() (k+1),
(k+1),
|PQ|=![]() (xQ-x)=-
(xQ-x)=-![]() ,
,
所以|PA|·|PQ|=-(k-1)(k+1)3,
令f(k)=-(k-1)(k+1)3,则f′(k)=-(4k-2)(k+1)2,
当k∈![]() 时,f′(k)>0;当k∈
时,f′(k)>0;当k∈![]() 时,f′(k)<0,
时,f′(k)<0,
所以f(k)在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减.
上单调递减.
因此当k=![]() 时,|PA|·|PQ|取得最大值
时,|PA|·|PQ|取得最大值![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的一个焦点与抛物线y2=-4x的焦点相同,且椭圆C上一点与椭圆C的左,右焦点F1,F2构成的三角形的周长为
的一个焦点与抛物线y2=-4x的焦点相同,且椭圆C上一点与椭圆C的左,右焦点F1,F2构成的三角形的周长为![]() .
.
(1)求椭圆C的方程;
(2)若直线l:y=kx+m(k,m∈R)与椭圆C交于A,B两点,O为坐标原点,△AOB的重心G满足: ![]() ,求实数m的取值范围.
,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|2x+3|-|2x-a|,a∈R.
(1)若不等式f(x)≤-5的解集非空,求实数a的取值范围;
(2)若函数y=f(x)的图象关于点![]() 对称,求实数a的值.
对称,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|2x+1|+|x+1|.
(Ⅰ)求不等式f(x)≤8的解集;
(Ⅱ)若不等式f(x)>|a-2|对任意x∈R恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数),以
为参数),以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() (其中
(其中![]() 为常数).
为常数).
(1)若直线![]() 与曲线
与曲线![]() 恰好有一个公共点,求实数
恰好有一个公共点,求实数![]() 的值;
的值;
(2)若![]() ,求直线
,求直线![]() 被曲线
被曲线![]() 截得的弦长.
截得的弦长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() .
.
(Ⅰ)若原点到直线x+y-b=0的距离为![]() ,求椭圆的方程;
,求椭圆的方程;
(Ⅱ)设过椭圆的右焦点且倾斜角为45°的直线l和椭圆交于A,B两点,对于椭圆上任意一点M,总存在实数λ、μ,使等式![]() 成立,求λ2+μ2的值.
成立,求λ2+μ2的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年1月,某国宣布成功进行氢弹试验后,A,B,C,D四国领导人及联合国主席纷纷表示谴责,就此,某电视台特别邀请一军事专家对这一事件进行评论,若该军事专家计划从A,B,C,D四国及联合国主席这5个领导人中任选2人的发言态度进行评论,那么,他评论的这2人中至少包括A、B一国领导人的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com