
【题目】已知直三棱柱ABC﹣A1B1C1的底面为正三角形,E,F分别是A1C1 , B1C1上的点,且满足A1E=EC1 , B1F=3FC1 . 
(1)求证:平面AEF⊥平面BB1C1C;
(2)设直三棱柱ABC﹣A1B1C1的棱长均相等,求二面角C1﹣AE﹣B的余弦值.
【答案】
(1)证明:取B1C1的中点G,连结A1G,
∵B1F=3FC1,FG=FC1,∴EF∥A1G,
在等边△A1B1C1中,由G是B1C1的中点,知A1G⊥B1C1,
∴EF⊥B1C1,
∵三棱柱ABC﹣A1B1C1是直棱柱,∴BB1⊥平面A1B1C1,
又∵EF平面A1B1C1,∴BB1⊥EF,
∵BB1∩B1C1=B1,∴EF⊥平面BB1C1C,
又EF平面AEF,∴平面AEF⊥平面BB1C1C
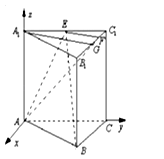
(2)解:(2)以A为坐标原点,以AA1,AC分别为y轴,z轴,建立空间直角坐标系,
设直三棱柱ABC﹣A1B1C1的棱均为2,则A(0,0,0),B( ![]() ),E(0,1,2),
),E(0,1,2),
∴ ![]() =(0,1,2),
=(0,1,2), ![]() =(
=( ![]() ),
),
设 ![]() =(x,y,z)是平面ABE的一个法向量,
=(x,y,z)是平面ABE的一个法向量,
由 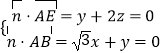 ,取x=﹣2,得
,取x=﹣2,得 ![]() =(﹣2,2
=(﹣2,2 ![]() ,﹣
,﹣ ![]() ),
),
平面AEC1的一个法向量 ![]() =(1,0,0),
=(1,0,0),
设二面角C1﹣AE﹣B的平面角为θ,
则cosθ= ![]() =
= ![]() .
.
∴二面角C1﹣AE﹣B的余弦值为 ![]() .
.

【解析】(1)取B1C1的中点G,连结A1G,推导出EF∥A1G,A1G⊥B1C1 , 从而EF⊥B1C1 , 由三棱柱ABC﹣A1B1C1是直棱柱,得到BB1⊥EF,从而EF⊥平面BB1C1C,由此能证明平面AEF⊥平面BB1C1C.(2)以A为坐标原点,以AA1 , AC分别为y轴,z轴,建立空间直角坐标系,利用向量法能求出二面角C1﹣AE﹣B的余弦值.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案科目:高中数学 来源: 题型:
【题目】已知a>0,b>0,函数f(x)=|x+a|+|2x﹣b|的最小值为1.
(1)求证:2a+b=2;
(2)若a+2b≥tab恒成立,求实数t的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面几种推理过程是演绎推理的是( )
A.某校高三(1)班有55人,2班有54人,3班有52人,由此得高三所有班人数超过50人
B.两条直线平行,同旁内角互补,如果∠A与∠B是两条平行直线的同旁内角,则∠A+∠B=180°
C.由平面三角形的性质,推测空间四边形的性质
D.在数列{an}中,a1=1,an= ![]() (an-1+
(an-1+ ![]() )(n≥2),由此归纳出{an}的通项公
)(n≥2),由此归纳出{an}的通项公
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xe2x﹣lnx﹣ax.
(1)当a=0时,求函数f(x)在[ ![]() ,1]上的最小值;
,1]上的最小值;
(2)若x>0,不等式f(x)≥1恒成立,求a的取值范围;
(3)若x>0,不等式f( ![]() )﹣1≥
)﹣1≥ ![]() e
e ![]() +
+ ![]() 恒成立,求a的取值范围.
恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究某药品的疗效,选取若干名志愿者进行临床试验,所有志愿者的舒张压数据(单位:![]() )的分组区间为
)的分组区间为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,将其按从左到右的顺序分别编号为第一组,第二组,
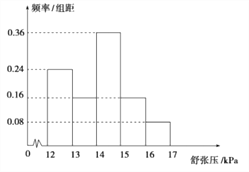
,将其按从左到右的顺序分别编号为第一组,第二组,![]() ,第五组,如图是根据试验数据制成的频率分布直方图,已知第一组与第二组共有20人,第三组没有疗效的有6人,则第三组中有疗效的人数为__________.
,第五组,如图是根据试验数据制成的频率分布直方图,已知第一组与第二组共有20人,第三组没有疗效的有6人,则第三组中有疗效的人数为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线 ![]() 的极坐标方程是
的极坐标方程是 ![]() ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为 ![]() 轴的正半轴,建立平面直角坐标系,在平面直角坐标系
轴的正半轴,建立平面直角坐标系,在平面直角坐标系 ![]() 中,直线
中,直线 ![]() 经过点
经过点 ![]() ,倾斜角
,倾斜角 ![]() .
.
(1)写出曲线 ![]() 的直角坐标方程和直线
的直角坐标方程和直线 ![]() 的参数方程;
的参数方程;
(2)设 ![]() 与曲线
与曲线 ![]() 相交于
相交于 ![]() ,
, ![]() 两点,求
两点,求 ![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com