练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    （理）有3张都标着字母R，5张分别标着数字1，2，3，4，5的卡片，若任取其中4张卡片组成牌号，则可以组成的不同牌号的总数等于 （用数字作答）
    （文）在5张分别标着数字1，2，3，4，5的卡片中，任取其中3张卡片，和3张都标着字母R的卡片一同组成牌号，则可以组成的不同牌号的总数等于（用数字作答）.
    500 ,1200

    本题考查排列组合的相关计算。理科题目中，可以分为字母R被取用0,1,2,3次4种情况，由加法原理，知
    文科题目中，可以看成先从5个数选出3个数（组合），再在6个位置中选出3个排列这三个数，得
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

    有3本不同的语文书和3本不同的数学书，求满足下列条件的方法总数（用数字作答）
    （1）6本排成一排；
    （2）6本排成一排，其中3本数学书必须相邻；
    （3）6本排成一排，其中语文书互不相邻.               

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

            

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    用1，2，3，4，5这五个数字组成无重复数字四位偶数，共有   ▲  个．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

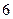    (1)个人坐在一排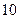个座位上,问①空位不相邻的坐法有多少种?② 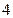个空位只有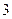个相邻的坐法有多少种?
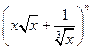    (2) 的展开式奇数项的二项式系数之和为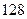，则求展开式中二项式系数最大项。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    已知，则的值等于     _．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题


    （本小题满分10分）
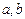    （I）两数的最大公约数为400，则两数的公约数的个数是       ；
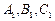    （II）某人有4种颜色的灯泡（每种颜色的灯泡足够多），要在如图所示的6个点A、B、C、上各装一个灯泡.要求同一条线段两端的灯泡不同色，则每种颜色的灯泡都至少用一个的安装方法共有       种（用数字作答）．

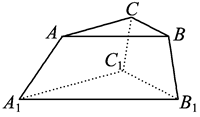
    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    袋中有10个球，其中7个红球，3个白球，任意取出3个，则其中所含白球的个数是
    A．0,1,2B．1,2,3C．2,3,4D．0,1,2,3

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

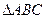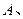
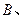
    内有任意三点不共线的2008个点，加上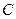三个顶点共2011个点，这2011个点的连线形成互不重叠的小三角形，则一共可以形成小三角形的个数为（   ）
    A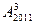．B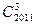．C．4017D．4019

    查看答案和解析>>

    同步练习册答案