
【题目】在某单位的食堂中,食堂每天以10元/斤的价格购进米粉,然后以4.4元/碗的价格出售,每碗内含米粉0.2斤,如果当天卖不完,剩下的米粉以2元/斤的价格卖给养猪场.根据以往统计资料,得到食堂某天米粉需求量的频率分布直方图如图所示,若食堂购进了80斤米粉,以![]() (斤)(其中
(斤)(其中![]() )表示米粉的需求量,
)表示米粉的需求量, ![]() (元)表示利润.
(元)表示利润.
(1)估计该天食堂利润不少于760元的概率;
(2)在直方图的需求量分组中,以区间中间值作为该区间的需求量,以需求量落入该区间的频率作为需求量在该区间的概率,求![]() 的分布列和数学期望.
的分布列和数学期望.

 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】将2张边长均为1分米的正方形纸片分别按甲、乙两种方式剪裁并废弃阴影部分.
(1)在图甲的方式下,剩余部分恰能完全覆盖某圆锥的表面,求该圆锥的母线长及底面
半径;
(2)在图乙的方式下,剩余部分能完全覆盖一个长方体的表面,求长方体体积的最大值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在梯形ABCD中,AD∥BC,AD⊥DC,BC=2AD,四边形ABEF是矩形,将矩形ABEF沿AB折起到四边形ABE1F1的位置,使平面ABE1F1⊥平面ABCD,M为AF1的中点,如图2.
(1)求证:BE1⊥DC;
(2)求证:DM∥平面BCE1;
(3)判断直线CD与ME1的位置关系,并说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校从参加安全知识竞赛的同学中,选取60名同学将其成绩(百分制,均为整数,成绩![]() 分记为优秀)分成6组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题:
分记为优秀)分成6组后,得到部分频率分布直方图(如图),观察图形中的信息,回答下列问题:
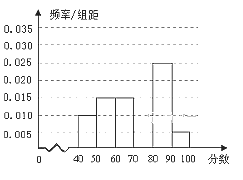
(1)求分数在[70,80)内的频率,并补全这个频率分布直方图;
(2)从频率分布直方图中,估计本次考试的平均分;
(3)为参加市里举办的安全知识竞赛,学校举办预选赛.已知在学校安全知识竞赛中优秀的同学通过预选赛的概率为![]() ,现在从学校安全知识竞赛中优秀的同学中选3人参加预选赛,若随机变量
,现在从学校安全知识竞赛中优秀的同学中选3人参加预选赛,若随机变量![]() 表示这3人中通过预选赛的人数,求
表示这3人中通过预选赛的人数,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,建立极坐标系,已知直线
轴的正半轴为极轴,建立极坐标系,已知直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)写出直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,点
两点,点![]() 为
为![]() 的中点,点
的中点,点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若椭圆C1: ![]() 和椭圆C2:
和椭圆C2: ![]() 的焦点相同且a1>a2.给出如下四个结论:
的焦点相同且a1>a2.给出如下四个结论:
①椭圆C1和椭圆C2一定没有公共点;
②![]() ;
;
③![]() ;
;
④a1-a2<b1-b2.
其中,所有正确结论的序号是( )
A. ②③④ B. ①③④
C. ①②④ D. ①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=a(x-lnx)+![]() ,a∈R.
,a∈R.
(I)讨论f(x)的单调性;
(II)当a=1时,证明f(x)>f’(x)+![]() 对于任意的x∈[1,2] 恒成立。
对于任意的x∈[1,2] 恒成立。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 的底面
的底面![]() 是直角梯形,
是直角梯形, ![]() ,
, ![]() ,
, ![]() ,点
,点![]() 在线段
在线段![]() 上,且
上,且![]() ,
, ![]() ,
, ![]() 平面
平面![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)当四棱锥![]() 的体积最大时,求平面
的体积最大时,求平面![]() 与平面
与平面![]() 所成二面角的余弦值.
所成二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com