
����Ŀ����Ҫ�������3��������飺
�ٴ�15�������г�ȡ5�ּ���Ƿ�ϸ�.
��������ij��ѧ����480����ְ��������һ�߽�ʦ360����������Ա48����������Ա72��.Ϊ�˽��ְ����ѧУУ���������������ȡһ������Ϊ20������.
��������ij��ѧ��������28�ţ�ÿ����35����λ��һ�α����ǡ�����������ڣ�����������Ϊ����ȡ�������Ҫ��28�����ڽ�����̸.
��Ϊ�����ij��������ǣ� ��
A. �ټ���������� ��ϵͳ������ �۷ֲ����
B. �ټ���������� �ڷֲ������ ��ϵͳ����
C. ��ϵͳ������ �ڼ���������� �۷ֲ����
D. �ٷֲ������ ��ϵͳ������ �ۼ��������

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ����ABC��A1B1C1�У�D��E�ֱ���AB��BB1���е㣬AA1=AC=CB= ![]() AB��
AB�� 
��1��֤����BC1��ƽ��A1CD
��2��������D��A1C��E������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������f��x��=x2+ax+ ![]() ������������a��ȡֵ��Χ�ǣ� ��
������������a��ȡֵ��Χ�ǣ� ��
A.[��1��0]
B.[��1����]
C.[0��3]
D.[3��+��]
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]() ��
��
��1����x��0ʱ��f��x����0����˵���Сֵ��
��2��������{an}��ͨ��an=1+ ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ֲ�Ʒ��4ֻ��Ʒ��6ֻ��Ʒ��ÿֻ��Ʒ������ͬ�ҿ����֣���ÿ��ȡ��һֻ�����ԣ�ֱ����4ֻ��Ʒȫ���Ϊֹ�������һֻ��Ʒǡ���ڵ���β���ʱ�����֣���ͬ���������______������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() ��ƽ�����ཻ��
��ƽ�����ཻ��![]() �ǵ��������� ��
�ǵ��������� ��![]() �ֱ���
�ֱ���![]() �ᣬ
�ᣬ![]() ��������ͬ��ĵ�λ������������
��������ͬ��ĵ�λ������������![]() �������������
�������������![]() ��������
��������![]() ������ϵ
������ϵ![]() �е����꣬����
�е����꣬����![]() .
.
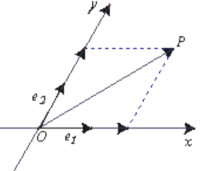
��1������![]() �Ĵ�С��
�Ĵ�С��
��2��������![]() ����
����![]() ��
��![]() ���ߣ���ʵ��
���ߣ���ʵ��![]() ��ֵ��
��ֵ��
��3���Ƿ����ʵ��![]() ��ʹ��
��ʹ��![]() ������
������![]() ��ֱ�����������
��ֱ�����������![]() ��ֵ������������˵������.
��ֵ������������˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ƽ������![]() ����
����![]() �����������ʱ�뷽����ת
�����������ʱ�뷽����ת![]() �ǵõ�����
�ǵõ�����![]() ��
��![]() �������ѵ�
�������ѵ�![]() �Ƶ�
�Ƶ�![]() ��ʱ�뷽����ת
��ʱ�뷽����ת![]() �ǵõ���
�ǵõ���![]() .
.
(1)��֪ƽ���ڵ�![]() ����
����![]() ���ѵ�
���ѵ�![]() �Ƶ�
�Ƶ�![]() ˳ʱ�뷽����ת
˳ʱ�뷽����ת![]() ��õ���
��õ���![]() �����
�����![]() �����ꣻ
�����ꣻ
(2)��ƽ��������![]() �ϵ�ÿһ��������ԭ������ʱ�뷽����ת
�ϵ�ÿһ��������ԭ������ʱ�뷽����ת![]() ��õ��ĵ�Ĺ켣����������
��õ��ĵ�Ĺ켣����������![]() ����ԭ������
����ԭ������![]() �ķ���.
�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��
��![]() �����ҽ���ֱ�Ϊ
�����ҽ���ֱ�Ϊ![]() ��
��![]() ����
����![]() �Ҵ�ֱ��
�Ҵ�ֱ��![]() ��Ľ����ҵ��ҳ�Ϊ
��Ľ����ҵ��ҳ�Ϊ![]() ����
����![]() ��ֱ��
��ֱ��![]() ����Բ
����Բ![]() ��
��![]() ��
��![]() ���㣬��
���㣬��![]() ���ܳ�Ϊ
���ܳ�Ϊ![]() .
.
��1������Բ![]() �ķ��̣�
�ķ��̣�
��2����ֱ֪��![]() ��
��![]() ���ഹֱ��ֱ��
���ഹֱ��ֱ��![]() ��
��![]() ������Բ
������Բ![]() ���ڵ�
���ڵ�![]() ��
��![]() ���㣬ֱ��
���㣬ֱ��![]() ��
��![]() ������Բ
������Բ![]() ����
����![]() ��
��![]() ����.��
����.��![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijͶ�ʹ�˾�ƻ�Ͷ��![]() ���ֽ��ڲ�Ʒ�������г�������Ԥ�⣬
���ֽ��ڲ�Ʒ�������г�������Ԥ�⣬![]() ��Ʒ������
��Ʒ������![]() ��Ͷ�ʽ��
��Ͷ�ʽ��![]() �ĺ�����ϵΪ
�ĺ�����ϵΪ![]() ��
��![]() ��Ʒ������
��Ʒ������![]() ��Ͷ�ʽ��
��Ͷ�ʽ��![]() �ĺ�����ϵΪ
�ĺ�����ϵΪ![]() ��ע��������Ͷ�ʽ�λ����Ԫ��.
��ע��������Ͷ�ʽ�λ����Ԫ��.
��1���ù�˾����100��Ԫ�ʽ𣬲��ƻ�ȫ��Ͷ��![]() ���ֲ�Ʒ�У�����
���ֲ�Ʒ�У�����![]() ��Ԫ�ʽ�Ͷ��
��Ԫ�ʽ�Ͷ��![]() ��Ʒ����
��Ʒ����![]() ���ֲ�Ʒ�����ܺ�
���ֲ�Ʒ�����ܺ�![]() ��ʾΪ
��ʾΪ![]() �ĺ�������д��������
�ĺ�������д��������
��2������������100��Ԫ�ʽ𣬲���ʹ��˾�������ܺ�![]() ����������������ܺ�Ϊ������Ԫ.
����������������ܺ�Ϊ������Ԫ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com