
【题目】已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为原点,极轴为
,以极点为原点,极轴为![]() 轴非负半轴建立平面直角坐标系,直线
轴非负半轴建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).
为参数).
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)在(1)中,设曲线![]() 经过伸缩变换
经过伸缩变换 得到曲线
得到曲线![]() ,设曲线
,设曲线![]() 上任意一点为
上任意一点为![]() ,当点
,当点![]() 到直线
到直线![]() 的距离取最大值时,求此时点
的距离取最大值时,求此时点![]() 的直角坐标.
的直角坐标.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
(1)由![]() 可将曲线
可将曲线![]() 的极坐标方程化为直角坐标方程,在直线
的极坐标方程化为直角坐标方程,在直线![]() 的参数方程中消去参数
的参数方程中消去参数![]() 可将直线
可将直线![]() 的参数方程化为普通方程;
的参数方程化为普通方程;
(2)利用伸缩变换求得曲线![]() 的普通方程,进而可得出曲线
的普通方程,进而可得出曲线![]() 的参数方程,设点
的参数方程,设点![]() ,利用点到直线的距离公式结合辅助角公式、正弦函数的有界性可求得点
,利用点到直线的距离公式结合辅助角公式、正弦函数的有界性可求得点![]() 到直线
到直线![]() 的距离的最大值,并求出对应的点
的距离的最大值,并求出对应的点![]() 的坐标.
的坐标.
(1)将曲线![]() 的极坐标方程化为
的极坐标方程化为![]() ,由
,由![]() ,
,
所以,曲线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
在直线![]() 的参数方程中消去参数
的参数方程中消去参数![]() 得
得![]() ,
,
所以,直线![]() 的普通方程为
的普通方程为![]() ;
;
(2)由伸缩变换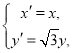 得
得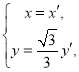 带入圆的方程
带入圆的方程![]() 得
得![]() ,
,
化简得曲线![]() ,其参数方程为
,其参数方程为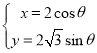 (
(![]() 为参数,且
为参数,且![]() ),
),
设点![]() ,
,
点![]() 到直线
到直线![]() 距离为:
距离为:
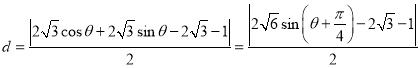 ,
,
![]() ,则
,则![]() ,所以,当
,所以,当![]() 时,即当
时,即当![]() 时,
时,
![]() 取最大值,即
取最大值,即![]() ,
,
此时,点![]() 的坐标为
的坐标为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图(如图①)、90后从事互联网行业岗位分布条形图(如图②),则下列结论中不一定正确的是( )
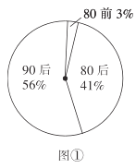
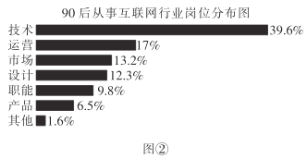
注:90后指1990年及以后出生,80后指1980~1989年之间出生,80前指1979年及以前出生.
A.互联网行业从业人员中90后占一半以上
B.互联网行业中从事技术岗位的人数超过总人数的20%
C.互联网行业中从事运营岗位的人数90后比80前多
D.互联网行业中从事技术岗位的人数90后比80后多
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 时代悄然来临,为了研究中国手机市场现状,中国信通院统计了2019年手机市场每月出货量以及与2018年当月同比增长的情况,得到如下统计图,根据该统计图,下列说法错误的是( )
时代悄然来临,为了研究中国手机市场现状,中国信通院统计了2019年手机市场每月出货量以及与2018年当月同比增长的情况,得到如下统计图,根据该统计图,下列说法错误的是( )
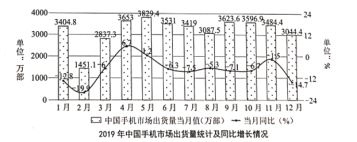
A.2019年全年手机市场出货量中,5月份出货量最多
B.2019年下半年手机市场各月份出货量相对于上半年各月份波动小
C.2019年全年手机市场总出货量低于2018年全年总出货量
D.2018年12月的手机出货量低于当年8月手机出货量
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】七巧板是中国古代劳动人民的发明,其历史至少可以追溯到公元前一世纪,后清陆以湉《冷庐杂识》卷一中写道“近又有七巧图,其式五,其数七,其变化之式多至千余”在18世纪,七巧板流传到了国外,被誉为“东方魔板”,至今英国剑桥大学的图书馆里还珍藏着一部《七巧新谱》.完整图案为一正方形(如图):五块等腰直角三角形、一块正方形和一块平行四边形,如果在此正方形中随机取一点,那么此点取自阴影部分的概率是( )
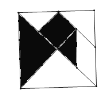
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)为奇函数,且当x≥0时,f(x)=ex﹣cosx,则不等式f(2x﹣1)+f(x﹣2)>0的解集为( )
A.(﹣∞,1)B.(﹣∞,![]() )C.(
)C.(![]() ,+∞)D.(1,+∞)
,+∞)D.(1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 过点
过点![]() ,
,![]() 、
、![]() 分别为椭圆C的左、右焦点且
分别为椭圆C的左、右焦点且![]()
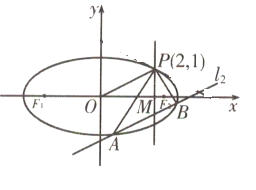
(1)求椭圆C的方程;
(2)直线![]() 平行于OP(O为原点),且与椭圆C交于两点A、B,与直线x=2交于点M(M介于A、B两点之间).
平行于OP(O为原点),且与椭圆C交于两点A、B,与直线x=2交于点M(M介于A、B两点之间).
(I)当△PAB面积最大时,求![]() 的方程;
的方程;
(II)求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过![]() 轴正半轴上一点
轴正半轴上一点![]() 做直线与抛物线
做直线与抛物线![]() 交于
交于![]() ,
,![]() ,
,![]() 两点,且满足
两点,且满足![]() ,过定点
,过定点![]() 与点
与点![]() 做直线
做直线![]() 与抛物线交于另一点
与抛物线交于另一点![]() ,过点
,过点![]() 与点
与点![]() 做直线
做直线![]() 与抛物线交于另一点
与抛物线交于另一点![]() .设三角形
.设三角形![]() 的面积为
的面积为![]() ,三角形
,三角形![]() 的面积为
的面积为![]() .
.
(1)求正实数![]() 的取值范围;
的取值范围;
(2)连接![]() ,
,![]() 两点,设直线
两点,设直线![]() 的斜率为
的斜率为![]() ;
;
(ⅰ)当![]() 时,直线
时,直线![]() 在
在![]() 轴的纵截距范围为
轴的纵截距范围为![]() ,则求
,则求![]() 的取值范围;
的取值范围;
(ⅱ)当实数![]() 在(1)取到的范围内取值时,求
在(1)取到的范围内取值时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com