练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如下图,已知△ABC是边长为1的正三角形,M\,N分别是边AB\,AC上的点,线段MN经过△ABC的中心G.设∠MGA=α(≤α≤).

    (1)试将△AGM,△AGN的面积(分别记为S1与S2)表示为α的函数;

    (2)求y=的最大值与最小值.

    解：(1)因为G是边长为1的正三角形ABC的中心，

    所以AG=,∠MAG=,

    由正弦定理，得GM=.

    则S1=GM·GA·sinα=,同理可求得S2=,

    (2)y===72(3+cot2a),

    因为≤α≤,所以当α=或α=时，y取得最大值ymax=240;

    当α=时，y取得最小值ymin=216.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：044

        如下图，已知△ABC的三边分别为a,b,c，A为圆心，直径PQ=2r，问P,Q在什么位置时，有最大值？

     

    查看答案和解析>>

    科目：高中数学 来源：数学教研室 题型：044

        如下图，已知△ABC的三边分别为a,b,c，A为圆心，直径PQ=2r，问P,Q在什么位置时，有最大值？

     

    查看答案和解析>>

    科目：高中数学 来源：学习周报　数学　北师大课标高一版(必修4)　2009－2010学年　第51期　总207期 北师大课标版 题型：044

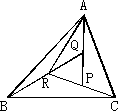
    如下图，已知△ABC所在平面内一点P，满足：AP的中点为Q，BQ的中点为R，CR的中点为P．设＝a，＝b，试用a，b表示向量．

    查看答案和解析>>

    科目：高中数学 来源：重难点手册　高中数学·必修4（配人教A版新课标） 人教A版新课标 题型：044

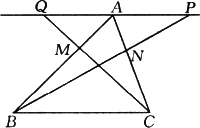
    如下图，已知△ABC中，点N在AC上，且AN＝AC，M在AB上，且AM＝AB，在BN的延长线上取点P，使NP＝BN，在CM的延长线上取点Q，使MQ＝CM，用向量方法证明：P、A、Q三点共线．

    查看答案和解析>>

    科目：高中数学 来源：2009年高考数学文科(海南卷) 题型：044

    选修4－1：几何证明选讲

    如下图，已知△ABC中的两条角平分线AD和CE相交于H，∠B＝60°，F在AC上，且AE＝AF．

    (Ⅰ)证明：B，D，H，E四点共圆：

    (Ⅱ)证明：CE平分∠DEF．

    查看答案和解析>>

    同步练习册答案