
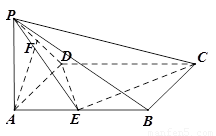
如图,已知在四棱锥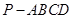 中,底面
中,底面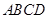 是矩形,
是矩形,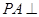 平面
平面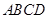 ,
,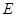 、
、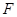 分别是
分别是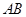 、
、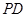 的中点.
的中点.
(Ⅰ)求证: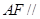 平面
平面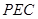 ;
;
(Ⅱ)若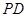 与平面
与平面 所成角为
所成角为 ,且
,且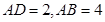 ,求点
,求点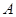 到平面
到平面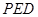 的距离.
的距离.
(1)见试题解析;(2) .
.
【解析】
试题分析:(I)要证明 平面
平面 ,关键是在平面
,关键是在平面 内找到一条与直线
内找到一条与直线 平行的直线,本题就想是否有一个过直线
平行的直线,本题就想是否有一个过直线 的平面与平面
的平面与平面 相交,交线就是我们要找的平行直线(可根据线面平行的性质定理知),在图形中可容易看出应该就是平面
相交,交线就是我们要找的平行直线(可根据线面平行的性质定理知),在图形中可容易看出应该就是平面 ,只不过再想一下,交线到底是什么而已,当然具体辅助线的作法也可换成另一种说法(即试题解析中的直接取
,只不过再想一下,交线到底是什么而已,当然具体辅助线的作法也可换成另一种说法(即试题解析中的直接取 中点
中点 ,然后连接
,然后连接 的方法);(2)由于
的方法);(2)由于 平面
平面 ,所以三棱锥
,所以三棱锥 的体积可以很快求出,从而本题可用体积法求点
的体积可以很快求出,从而本题可用体积法求点 到平面
到平面 的距离,另外由于
的距离,另外由于 ,如果取
,如果取 中点
中点 ,则有
,则有 ,从而可得
,从而可得 平面
平面 ,也即平面
,也即平面
 平面
平面 ,这时点
,这时点 到平面
到平面 的垂线段可很快作出,从而迅速求出结论.
的垂线段可很快作出,从而迅速求出结论.
试题解析:(I)证明:如图,取 的中点
的中点 ,连接
,连接 .
.

由已知得 且
且 ,
,
又 是
是 的中点,则
的中点,则 且
且 ,
, 是平行四边形, ∴
是平行四边形, ∴
又 平面
平面 ,
, 平面
平面
 平面
平面
(II)设 平面
平面 的距离为
的距离为 ,
,
【法一】:因 平面
平面 ,故
,故 为
为 与平面
与平面 所成角,所以
所成角,所以 ,
,
所以 ,
, ,又因
,又因 ,
, 是
是 的中点所以
的中点所以 ,
, ,
, .
.
作 于
于 ,因
,因 ,则
,则
 ,
,
则 ,
,
因 所以
所以
【法二】因 平面
平面 ,故
,故 为
为 与平面
与平面 所成角,所以
所成角,所以 ,
,
所以 ,
, ,又因
,又因 ,
, 是
是 的中点所以
的中点所以 ,
, ,
, .
.
作 于
于 ,连结
,连结 ,因
,因 ,则
,则 为
为 的中点,故
的中点,故
所以 平面
平面 ,所以平面
,所以平面 平面
平面 ,作
,作 于
于 ,则
,则 平面
平面 ,所以线段
,所以线段 的长为
的长为 平面
平面 的距离.
的距离.
又 ,
,
所以 .
.
考点:(1)线面平行的判定;(2)点到平面的距离.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
 如图,已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E、F分别是AB、PD的中点.
如图,已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E、F分别是AB、PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知在四棱锥P-ABCD中,底面ABCD是菱形,PA⊥底面ABCD,AB=1,PA•AC=1,∠ABC=θ(0<θ<
如图,已知在四棱锥P-ABCD中,底面ABCD是菱形,PA⊥底面ABCD,AB=1,PA•AC=1,∠ABC=θ(0<θ<| π | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
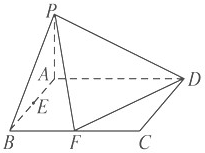 如图,已知在四棱锥PABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E,F分别是线段AB,BC的中点.
如图,已知在四棱锥PABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E,F分别是线段AB,BC的中点.查看答案和解析>>
科目:高中数学 来源:2012-2013学年贵州省六高三第一次考理科数学试卷(解析版) 题型:解答题
(本小题满分12分)如图 ,已知在四棱锥
,已知在四棱锥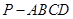 中,底面
中,底面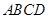 是矩形,
是矩形,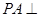 平面
平面 ,
,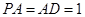 ,
,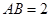 ,
,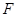 是
是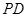 的中点,
的中点, 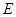 是线段
是线段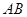 上的点.
上的点.
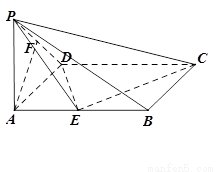
(I)当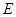 是
是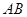 的中点时,求证:
的中点时,求证: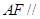 平面
平面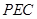 ;
;
(II)要使二面角 的大小为
的大小为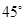 ,试确定
,试确定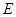 点的位置.
点的位置.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com