
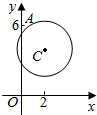
 ��֪ij��Ұ�����������ͻ���û����λ����Ϊ����·������������A���������y�Ḻ������ֱ�ߣ�������ð�մ�ԽҰ����������ͼ�����ϻ���û������ΪԲC����x-2��2+��y-4��2=$\frac{25}{4}$����������λ�����A��0��6����O��Ҫ40min������λ�������ϻ���û�ĵ�������ʱ�䳬��15min��������Σ�գ��ʣ���λ�����Ƿ�������Σ�գ���������λ���������ٷ���������
��֪ij��Ұ�����������ͻ���û����λ����Ϊ����·������������A���������y�Ḻ������ֱ�ߣ�������ð�մ�ԽҰ����������ͼ�����ϻ���û������ΪԲC����x-2��2+��y-4��2=$\frac{25}{4}$����������λ�����A��0��6����O��Ҫ40min������λ�������ϻ���û�ĵ�������ʱ�䳬��15min��������Σ�գ��ʣ���λ�����Ƿ�������Σ�գ���������λ���������ٷ��������� ���� �����⣬��λ����1min�߹���·��Ϊ$\frac{3}{20}$��15min�߹���·��Ϊ$\frac{9}{4}$�����Բ��y��صõ��ҳ�Ϊ3�����ɵó����ۣ�
��� �⣺�����⣬��λ����1min�߹���·��Ϊ$\frac{3}{20}$��15min�߹���·��Ϊ$\frac{9}{4}$��
ԲC����x-2��2+��y-4��2=$\frac{25}{4}$����x=0���ɵ�y=4��$\frac{3}{2}$��
��Բ��y��صõ��ҳ�Ϊ3��$\frac{9}{4}$��
����λ����������Σ�գ�
���� ���⿼��ֱ����Բ��λ�ù�ϵ������ѧ��������ѧ֪ʶ���ʵ������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [-1��0] | B�� | [0��1] | C�� | [1��3] | D�� | [1��4] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $3-2\sqrt{2}$ | B�� | $-3+2\sqrt{2}$ | C�� | $-3��2\sqrt{2}$ | D�� | $3��2\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{2+\sqrt{2}}}{2}$ | B�� | $2+\sqrt{2}$ | C�� | $1+\sqrt{2}$ | D�� | $\frac{{1+\sqrt{2}}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��x��Ǹ�����ƽ�֡�AOB����AOx=������ԲP��OA������MN=2a����OB������SQ=2b������ԲԲ��P�Ĺ켣���̣�
��ͼ��x��Ǹ�����ƽ�֡�AOB����AOx=������ԲP��OA������MN=2a����OB������SQ=2b������ԲԲ��P�Ĺ켣���̣��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com