
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 在
在![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围;
的取值范围;
(3)证明:当![]() 时,不等式
时,不等式![]() 成立.
成立.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)证明见解析
;(3)证明见解析
【解析】
(1)当![]() 时,
时,![]() ,
,![]() ,故切线为
,故切线为![]()
(2)由题意得:![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 恒成立,求
恒成立,求![]() 的最小值,即可得出答案.
的最小值,即可得出答案.
(3)当![]() 时,可证明
时,可证明![]() 恒成立,变形得:
恒成立,变形得:![]() ,
,
又因为![]() ,即
,即![]() ,故
,故![]() ,将
,将![]() 替换成
替换成![]() ,即可得出答案.
,即可得出答案.
解:(1)![]() 时,
时,![]() ,∴
,∴![]() ,
,
∴![]() ,
,![]() ,
,
∴切线方程为![]() .
.
(2)由题可知![]() 在
在![]() 上恒成立,
上恒成立,
∴![]() 恒成立,
恒成立,
设函数![]() ,则
,则![]() ,
,
令![]() 得
得![]() ,
,
当![]() 时
时![]() ,当
,当![]() 时
时![]() ,
,
∴![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,
单调递增,
∴![]() .
.
∴![]() ,∴
,∴![]() 的取值范围是
的取值范围是![]() .
.
(3)首先证明:当![]() 时,
时,![]() .
.
设![]() ,则
,则![]() ,
,![]() .
.
易得:![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
又![]() ,
,![]() ,
,![]() ,∴
,∴![]() .
.
所以存在![]() 使得
使得![]() .
.
∴当![]() 时
时![]() ,当
,当![]() 时
时![]() ,
,
当![]() 时
时![]() .
.
∴![]() 在
在![]() ,
,![]() 单调递增,在
单调递增,在![]() 单调递减,
单调递减,
∵![]() ,∴
,∴![]() 在
在![]() 都成立,
都成立,
即![]() 时
时![]() 恒成立.
恒成立.
即:![]() ,变形得:
,变形得:![]() ,
,
设![]() ,
,![]() ,
,![]() ,
,
∵当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
将![]() 替换成
替换成![]() 得:
得:![]() .
.


科目:高中数学 来源: 题型:
【题目】“中国剩余定理”又称“孙子定理”,最早可见于中国南北朝时期的数学著作《孙子算经》卷下第二十六题,叫做“物不知数”,原文如下:今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二.问物几何?现有这样一个相关的问题:将1到2020这2020个自然数中被5除余3且被7除余2的数按照从小到大的顺序排成一列,构成一个数列,则该数列各项之和为( )
A.56383B.57171C.59189D.61242
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是一个单调递增的等比数列,
是一个单调递增的等比数列,![]() 是一个等差数列,
是一个等差数列,![]() 是
是![]() 的前
的前![]() 项和,其中
项和,其中![]() ,
,![]() ,
,![]() 成等差数列,
成等差数列,![]() .
.
(1)求![]() 的通项公式;
的通项公式;
(2)若![]() ,
,![]() ,
,![]() 既成等比数列,又成等差数列.
既成等比数列,又成等差数列.
(i)求![]() 的通项公式;
的通项公式;
(ii)对于数列![]() ,若
,若![]() 且
且![]() ,或
,或![]() 且
且![]() ,则
,则![]() 为数列
为数列![]() 的转折点,求
的转折点,求![]() 的转折点个数.
的转折点个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三(1)班在一次语文测试结束后,发现同学们在背诵内容方面失分较为严重.为了提升背诵效果,班主任倡议大家在早晩读时间站起来大声诵读,为了解同学们对站起来大声诵读的态度,对全班50名同学进行调查,将调查结果进行整理后制成如表:
考试分数 |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 5 | 10 | 5 |
赞成人数 | 4 | 6 | 9 | 3 | 6 | 4 |
(1)欲使测试优秀率为![]() ,则优秀分数线应定为多少分?
,则优秀分数线应定为多少分?
(2)依据第1问的结果及样本数据研究是否赞成站起来大声诵读的态度与考试成绩是否优秀的关系,列出2×2列联表,并判断是否有![]() 的把握认为赞成与否的态度与成绩是否优秀有关系.
的把握认为赞成与否的态度与成绩是否优秀有关系.
参考公式及数据: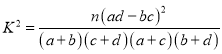 ,
,![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 过点
过点![]() ,且与
,且与![]() 内切,设
内切,设![]() 的圆心
的圆心![]() 的轨迹为
的轨迹为![]() ,
,
(1)求轨迹C的方程;
(2)设直线![]() 不经过点
不经过点![]() 且与曲线
且与曲线![]() 交于点
交于点![]() 两点,若直线
两点,若直线![]() 与直线
与直线![]() 的斜率之积为
的斜率之积为![]() ,判断直线
,判断直线![]() 是否过定点,若过定点,求出此定点的坐标,若不过定点,请说明理由.
是否过定点,若过定点,求出此定点的坐标,若不过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中“勾股容方”问题:“今有勾五步,股十二步,问勾中容方几何?”魏晋时期数学家刘徽在其《九章算术注》中利用出入相补原理给出了这个问题的一般解法:如图1,用对角线将长和宽分别为![]() 和
和![]() 的矩形分成两个直角三角形,每个直角三角形再分成一个内接正方形(黄)和两个小直角三角形(朱、青).将三种颜色的图形进行重组,得到如图2所示的矩形.该矩形长为
的矩形分成两个直角三角形,每个直角三角形再分成一个内接正方形(黄)和两个小直角三角形(朱、青).将三种颜色的图形进行重组,得到如图2所示的矩形.该矩形长为![]() ,宽为内接正方形的边长
,宽为内接正方形的边长![]() .由刘徽构造的图形还可以得到许多重要的结论,如图3.设
.由刘徽构造的图形还可以得到许多重要的结论,如图3.设![]() 为斜边
为斜边![]() 的中点,作直角三角形
的中点,作直角三角形![]() 的内接正方形对角线
的内接正方形对角线![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,则下列推理正确的是( )
,则下列推理正确的是( )
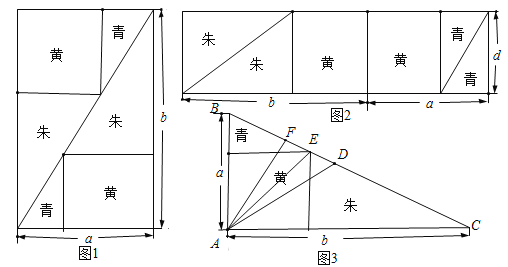
①由图1和图2面积相等得![]() ;
;
②由![]() 可得
可得![]() ;
;
③由![]() 可得
可得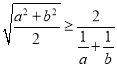 ;
;
④由![]() 可得
可得![]() .
.
A.①②③④B.①②④C.②③④D.①③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在
在![]() 处取得极值A,函数
处取得极值A,函数![]() ,其中
,其中![]() …是自然对数的底数.
…是自然对数的底数.
(1)求m的值,并判断A是![]() 的最大值还是最小值;
的最大值还是最小值;
(2)求![]() 的单调区间;
的单调区间;
(3)证明:对于任意正整数n,不等式![]() 成立.
成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)![]() (cosθ+1)cos2x+cosθ(cosx+1),有下述四个结论:①f(x)是偶函数;②f(x)在(
(cosθ+1)cos2x+cosθ(cosx+1),有下述四个结论:①f(x)是偶函数;②f(x)在(![]() ,
,![]() )上单调递减;③当θ∈[
)上单调递减;③当θ∈[![]() ,
,![]() ]时,有|f(x)|
]时,有|f(x)|![]() ;④当θ∈[
;④当θ∈[![]() ,
,![]() ]时,有|f'(x)|
]时,有|f'(x)|![]() ;其中所有真命题的编号是( )
;其中所有真命题的编号是( )
A.①③B.②④C.①③④D.①④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com