练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】松、竹、梅经冬不衰，因此有“岁寒三友”之称.在我国古代的诗词和典籍中有很多与松和竹相关的描述和记载，宋代刘学箕的《念奴娇·水轩沙岸》的“缀松黏竹，恍然如对三绝”描写了大雪后松竹并生相依的美景；宋元时期数学名著《算学启蒙》中亦有关于“松竹并生”的问题：松长五尺，竹长两尺，松日自半，竹日自倍，松竹何日而长等.现欲知几日后，竹长超过松长一倍.为了解决这个新问题，设计下面的程序框图，若输入的，，则输出的的值为（ ）

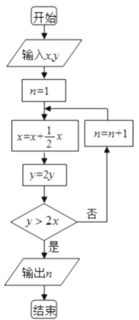
    A.4B.5C.6D.7

    【答案】A

    【解析】

    由已知中的程序框图可知：该程序的功能是利用循环结构计算并输出变量的值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得答案．

    解：当时，，，满足进行循环的条件，

    当时，，满足进行循环的条件，

    当时，，满足进行循环的条件，

    当时，，不满足进行循环的条件，

    故输出的值4．

    故选：A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在考察疫情防控工作中，某区卫生防控中心提出了“要坚持开展爱国卫生运动，从人居环境改善、饮食习惯、社会心理健康、公共卫生设施等多个方面开展，特别是要坚决杜绝食用野生动物的陋习，提倡文明健康、绿色环保的生活方式”的要求.某小组通过问卷调查，随机收集了该区居民六类日常生活习惯的有关数据.六类习惯是：（1）卫生习惯状况类；（2）垃圾处理状况类；（3）体育锻炼状况类；（4）心理健康状况类；（5）膳食合理状况类；（6）作息规律状况类.经过数据整理，得到下表：

    卫生习惯状况类

    垃圾处理状况类

    体育锻炼状况类

    心理健康状况类

    膳食合理状况类

    作息规律状况类

    有效答卷份数

    380

    550

    330

    410

    400

    430

    习惯良好频率

    0.6

    0.9

    0.8

    0.7

    0.65

    0.6

    假设每份调查问卷只调查上述六类状况之一，各类调查是否达到良好标准相互独立.

    （1）从小组收集的有效答卷中随机选取1份，求这份试卷的调查结果是膳食合理状况类中习惯良好者的概率；

    （2）从该区任选一位居民，试估计他在“卫生习惯状况类、体育锻炼状况类、膳食合理状况类”三类习惯方面，至少具备两类良好习惯的概率；

    （3）利用上述六类习惯调查的排序，用“”表示任选一位第k类受访者是习惯良好者，“”表示任选一位第k类受访者不是习惯良好者（）.写出方差，，，，，的大小关系.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某市环保部门对该市市民进行了一次垃圾分类知识的网络问卷调查，每位市民仅有一次参加机会，通过随机抽样，得到参与问卷调查的100人的得分（满分：100分）数据，统计结果如表所示：

    组别

    男

    2

    3

    5

    15

    18

    12

    女

    0

    5

    10

    10

    7

    13

    (1)若规定问卷得分不低于70分的市民称为“环保关注者”，请完成答题卡中的列联表，并判断能否在犯错误概率不超过0.05的前提下，认为是否为“环保关注者”与性别有关？

    (2)若问卷得分不低于80分的人称为“环保达人”．视频率为概率．

    ①在我市所有“环保达人”中，随机抽取3人，求抽取的3人中，既有男“环保达人”又有女“环保达人”的概率；

    ②为了鼓励市民关注环保，针对此次的调查制定了如下奖励方案：“环保达人”获得两次抽奖活动；其他参与的市民获得一次抽奖活动．每次抽奖获得红包的金额和对应的概率.如下表：

    红包金额（单位：元）

    10

    20

    概率

    现某市民要参加此次问卷调查，记（单位：元）为该市民参加间卷调查获得的红包金额，求的分布列及数学期望．

    附表及公式：

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示的几何体中，底面为菱形， ， ， 与相交于点，四边形为直角梯形， ， ， ，平面底面.

    （1）证明：平面平面；

    （2）求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】四棱锥中，面，底面为菱形，且有，，，为中点．

    （1）证明：面；

    （2）求二面角的平面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】从抛物线上各点向x轴作垂线，垂线段中点的轨迹为E.

    （1）求曲线E的方程；

    （2）若直线与曲线E相交于A，B两点，求证：；

    （3）若点F为曲线E的焦点，过点的直线与曲线E交于M，N两点，直线，分别与曲线E交于C，D两点，设直线，斜率分别为，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥中，四边形是矩形，，，为正三角形，且平面平面，、分别为、的中点.

    （1）证明：平面；

    （2）求几何体的体积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】有一个长方形木块，三个侧面积分别为8，12，24，现将其削成一个正四面体模型，则该正四面体模型棱长的最大值为（ ）

    A.2B.C.4D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】诚信是立身之本，道德之基，我校学生会创设了“诚信水站”，既便于学生用水，又推进诚信教育，并用“”表示每周“水站诚信度”，为了便于数据分析，以四周为一周期，如表为该水站连续十二周（共三个周期）的诚信数据统计：

    第一周

    第二周

    第三周

    第四周

    第一周期

    第二周期

    第三周期

    （Ⅰ）计算表中十二周“水站诚信度”的平均数；

    （Ⅱ）若定义水站诚信度高于的为“高诚信度”，以下为“一般信度”则从每个周期的前两周中随机抽取两周进行调研，计算恰有两周是“高诚信度”的概率；

    （Ⅲ）已知学生会分别在第一个周期的第四周末和第二个周期的第四周末各举行了一次“以诚信为本”的主题教育活动，根据已有数据，说明两次主题教育活动的宣传效果，并根据已有数据陈述理由.

    查看答案和解析>>

    同步练习册答案