
【题目】设函数![]()
(1)判断![]() 的单调性;
的单调性;
(2)当![]() 在
在![]() 上恒成立时,求
上恒成立时,求![]() 的取值范围;
的取值范围;
(3)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最小值.
上的最小值.
【答案】(1)见解析(2)![]() (3)当
(3)当![]() 时,最小值是
时,最小值是![]() ;当
;当![]() 时,最小值是
时,最小值是![]() .
.
【解析】
(1)首先求出函数![]() 的导数,对
的导数,对![]() 讨论,分
讨论,分![]() ,
,![]() ,得
,得![]() 的正负,可求出单调区间;
的正负,可求出单调区间;
(2)应用参数分离得![]() ,求出
,求出![]() 在
在![]() 上的最大值,只要
上的最大值,只要![]() 大于最大值即可;
大于最大值即可;
(3)由导函数,对![]() 分类讨论,可确定
分类讨论,可确定![]() 在区间
在区间![]() 上的单调性,从而确定最小值.
上的单调性,从而确定最小值.
(1)![]() ,
,![]() ,
,![]() ;
;![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() ,
,![]() ;
;![]() ,
,![]() ;所以
;所以![]() 在
在![]() 上单调递增;
上单调递增;![]() 在
在![]() 上单调递减.
上单调递减.
(2)![]() 在
在![]() 上恒成立,因为
上恒成立,因为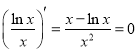 ,
,![]()
当![]() ,
,![]() ;当
;当![]() 时,
时,![]() ;所以
;所以![]()
即![]() .
.
(3)由(1)![]() ,
,![]() ,
,
①当![]() ,即
,即![]() 时,函数
时,函数![]() 在区间
在区间![]() 上是减函数,
上是减函数,
所以![]() 的最小值是
的最小值是![]()
②当![]() ,即
,即![]() 时,函数
时,函数![]() 在区间
在区间![]() 上是增函数,
上是增函数,
所以![]() 的最小值是
的最小值是![]() .
.
③当![]() ,即
,即![]() 时,函数
时,函数![]() 在区间
在区间![]() 上是增函数,在区间
上是增函数,在区间![]() 上是减函数,
上是减函数,
又![]() .
.
所以当![]() 时,最小值是
时,最小值是![]() ;
;
当![]() 时,最小值是.
时,最小值是.
综上可知,当![]() 时,最小值是
时,最小值是![]() ;当
;当![]() 时,最小值是
时,最小值是![]() .
.


科目:高中数学 来源: 题型:
【题目】为了整顿道路交通秩序,某地考虑将对行人闯红灯进行处罚.为了更好地了解市民的态度,在普通行人中随机选取了200人进行调查,当不处罚时,有80人会闯红灯,处罚时,得到如表数据:
处罚金额 | 5 | 10 | 15 | 20 |
会闯红灯的人数 | 50 | 40 | 20 | 10 |
若用表中数据所得频率代替概率.
(1)当罚金定为10元时,行人闯红灯的概率会比不进行处罚降低多少?
(2)将选取的200人中会闯红灯的市民分为两类:![]() 类市民在罚金不超过10元时就会改正行为;
类市民在罚金不超过10元时就会改正行为;![]() 类是其他市民.现对
类是其他市民.现对![]() 类与
类与![]() 类市民按分层抽样的方法抽取4人依次进行深度问卷,则前两位均为
类市民按分层抽样的方法抽取4人依次进行深度问卷,则前两位均为![]() 类市民的概率是多少?
类市民的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 的最大值为
的最大值为![]() .
.
(Ⅰ)求实数![]() 的值;
的值;
(Ⅱ)当![]() 时,讨论函数
时,讨论函数![]() 的单调性;
的单调性;
(Ⅲ)当![]() 时,令
时,令![]() ,是否存在区间
,是否存在区间![]() .使得函数
.使得函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() 若存在,求实数
若存在,求实数![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中实数a为常数.
,其中实数a为常数.
(I)当a=-l时,确定![]() 的单调区间:
的单调区间:
(II)若f(x)在区间![]() (e为自然对数的底数)上的最大值为-3,求a的值;
(e为自然对数的底数)上的最大值为-3,求a的值;
(Ⅲ)当a=-1时,证明![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2021年起,新高考科目设置采用“![]() ”模式,普通高中学生从高一升高二时将面临着选择物理还是历史的问题,某校抽取了部分男、女学生调查选科意向,制作出如右图等高条形图,现给出下列结论:
”模式,普通高中学生从高一升高二时将面临着选择物理还是历史的问题,某校抽取了部分男、女学生调查选科意向,制作出如右图等高条形图,现给出下列结论:
①样本中的女生更倾向于选历史;
②样本中的男生更倾向于选物理;
③样本中的男生和女生数量一样多;
④样本中意向物理的学生数量多于意向历史的学生数量.
根据两幅条形图的信息,可以判断上述结论正确的有( )


A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com