
【题目】已知函数![]() 在区间
在区间![]() 上是单调函数.
上是单调函数.
(1)求实数![]() 的所有取值组成的集合
的所有取值组成的集合![]() ;
;
(2)试写出![]() 在区间
在区间![]() 上的最大值
上的最大值![]() ;
;
(3)设![]() ,令
,令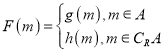 ,若对任意
,若对任意![]() ,总有
,总有![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)因为![]() 为开口向上的二次函数,故其在对称轴左边单调递减,对称轴右边单调递增. 函数在区间
为开口向上的二次函数,故其在对称轴左边单调递减,对称轴右边单调递增. 函数在区间![]() 上是单调函数,等价于区间
上是单调函数,等价于区间![]() 在对称轴的左边或者右边.列出不等式解出即可.
在对称轴的左边或者右边.列出不等式解出即可.
(2)讨论![]() 在
在![]() 上的单调性,分别求出其最大值,再写成分段函数的形式即可.
上的单调性,分别求出其最大值,再写成分段函数的形式即可.
(3)根据题意写出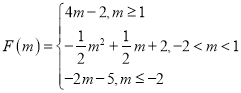 ,对任意
,对任意![]() ,总有
,总有![]() 等价于
等价于![]() 且
且![]() ,则分别讨论
,则分别讨论![]() 与
与 ![]() 的大小关系,找到其对应的
的大小关系,找到其对应的![]() 与
与![]() ,代入
,代入![]() 即可解出答案.
即可解出答案.
解:(1)对称轴![]() .
.
所以![]() 或
或![]() .
.
(2)①当![]() ,即
,即![]() 时.
时.
函数![]() 在
在![]() 上单调递增.
上单调递增.
所以![]() .
.
②当![]() ,即
,即![]() 时.
时.
函数![]() 在
在![]() 上单调递减.
上单调递减.
所以![]() .
.
综上所述:![]() .
.
(3)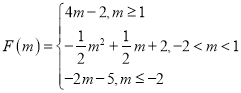 .
.
由题意得![]() ,
,![]() ,
,
画出函数![]() 的图像:
的图像:
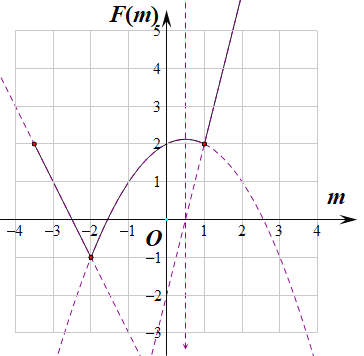
①当![]() 时,
时,![]() 在
在![]() 单调递减.
单调递减.
所以![]() ,
,![]() .
.
代入![]() ,解得
,解得![]() ,舍.
,舍.
②当![]() 时,
时,![]() 在
在![]() 单调递减,在
单调递减,在![]() 上单调递增.
上单调递增. ![]() ,
,![]() .
.
代入![]() ,解得
,解得![]() ,所以
,所以![]() ,
,
③当![]() 时,
时,![]() 在
在![]() 单调递减,在
单调递减,在![]() 上单调递增.
上单调递增. ![]() ,
, ![]() .
.
代入![]() ,化简得
,化简得![]() ,解得
,解得![]() 或
或![]() ,
,
所以![]() .
.
④当![]() 时,
时,![]() 在
在![]() 单调递减,在
单调递减,在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
![]() ,
,![]() .
.
代入![]() ,解得
,解得![]() ,所以
,所以![]() ,
,
⑤当![]() 时,
时,![]() 在
在![]() 单调递减,在
单调递减,在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
![]() ,
,![]() .
.
代入![]() ,解得
,解得![]() ,
,
综上所述:![]() .即
.即![]() .
.


科目:高中数学 来源: 题型:
【题目】在如图的程序框图中,若输入![]() ,
,![]() ,则输出的
,则输出的![]() 值是( )
值是( )
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/3/21/1907086498037760/1907898837975040/STEM/25d20caaa911497ea3baaf4f7dee45a3.png]
A. 3 B. 7 C. 11 D. 33
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在R上的奇函数,其中
是定义在R上的奇函数,其中![]() 为指数函数,且
为指数函数,且![]() 的图象过定点
的图象过定点![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)若关于x的方程,![]() 有解,求实数a的取值范围;
有解,求实数a的取值范围;
(3)若对任意的![]() ,不等式
,不等式![]() 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,中美贸易摩擦不断.特别是美国对我国华为的限制.尽管美国对华为极力封锁,百般刁难,并不断加大对各国的施压,拉拢他们抵制华为5G,然而这并没有让华为却步.华为在2018年不仅净利润创下记录,海外增长同样强劲.今年,我国华为某一企业为了进一步增加市场竞争力,计划在2020年利用新技术生产某款新手机.通过市场分析,生产此款手机全年需投入固定成本250万,每生产![]() (千部)手机,需另投入成本
(千部)手机,需另投入成本![]() 万元,且
万元,且  ,由市场调研知,每部手机售价0.7万元,且全年内生产的手机当年能全部销售完.
,由市场调研知,每部手机售价0.7万元,且全年内生产的手机当年能全部销售完.
(![]() )求出2020年的利润
)求出2020年的利润![]() (万元)关于年产量
(万元)关于年产量![]() (千部)的函数关系式,(利润=销售额—成本);
(千部)的函数关系式,(利润=销售额—成本);
![]() 2020年产量为多少(千部)时,企业所获利润最大?最大利润是多少?
2020年产量为多少(千部)时,企业所获利润最大?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形![]() 是菱形,
是菱形,![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.

(1)求证:![]() ∥平面
∥平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使二面角
,使二面角![]() 的大小为
的大小为![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,四边形
中,四边形![]() 是菱形,
是菱形,![]() 交BD于点
交BD于点![]() ,
,![]() 是边长为2的正三角形,
是边长为2的正三角形,![]() 分别是
分别是![]() 的中点.
的中点.

(1)求证:EF//平面SAD;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农业合作社生产了一种绿色蔬菜共![]() 吨,如果在市场上直接销售,每吨可获利
吨,如果在市场上直接销售,每吨可获利![]() 万元;如果进行精加工后销售,每吨可获利
万元;如果进行精加工后销售,每吨可获利![]() 万元,但需另外支付一定的加工费,总的加工
万元,但需另外支付一定的加工费,总的加工![]() (万元)与精加工的蔬菜量
(万元)与精加工的蔬菜量![]() (吨)有如下关系:
(吨)有如下关系: 设该农业合作社将
设该农业合作社将![]() (吨)蔬菜进行精加工后销售,其余在市场上直接销售,所得总利润(扣除加工费)为
(吨)蔬菜进行精加工后销售,其余在市场上直接销售,所得总利润(扣除加工费)为![]() (万元).
(万元).
(1)写出![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)当精加工蔬菜多少吨时,总利润最大,并求出最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com