
【题目】2019年12月以来,湖北武汉市发现多起病毒性肺炎病例,并迅速在全国范围内开始传播,专家组认为,本次病毒性肺炎病例的病原体初步判定为新型冠状病毒,该病毒存在人与人之间的传染,可以通过与患者的密切接触进行传染.我们把与患者有过密切接触的人群称为密切接触者,每位密切接触者被感染后即被称为患者.已知每位密切接触者在接触一个患者后被感染的概率为![]() ,某位患者在隔离之前,每天有
,某位患者在隔离之前,每天有![]() 位密切接触者,其中被感染的人数为
位密切接触者,其中被感染的人数为![]() ,假设每位密切接触者不再接触其他患者.
,假设每位密切接触者不再接触其他患者.
(1)求一天内被感染人数为![]() 的概率
的概率![]() 与
与![]() 、
、![]() 的关系式和
的关系式和![]() 的数学期望;
的数学期望;
(2)该病毒在进入人体后有14天的潜伏期,在这14天的潜伏期内患者无任何症状,为病毒传播的最佳时间,设每位患者在被感染后的第二天又有![]() 位密切接触者,从某一名患者被感染,按第1天算起,第
位密切接触者,从某一名患者被感染,按第1天算起,第![]() 天新增患者的数学期望记为
天新增患者的数学期望记为![]() .
.
(i)求数列![]() 的通项公式,并证明数列
的通项公式,并证明数列![]() 为等比数列;
为等比数列;
(ii)若戴口罩能降低每位密切接触者患病概率,降低后的患病概率![]() ,当
,当![]() 取最大值时,计算此时
取最大值时,计算此时![]() 所对应的
所对应的![]() 值和此时
值和此时![]() 对应的
对应的![]() 值,根据计算结果说明戴口罩的必要性.(取
值,根据计算结果说明戴口罩的必要性.(取![]() )
)
(结果保留整数,参考数据:![]() )
)
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 是函数y=f(x)的导函数,定义
是函数y=f(x)的导函数,定义![]() 为
为![]() 的导函数,若方程
的导函数,若方程![]() =0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的拐点,经研究发现,所有的三次函数f(x)=ax3+bx2+cx+d(a≠0)都有拐点,且都有对称中心,其拐点就是对称中心,设f(x)=x3﹣3x2﹣3x+6,则f(
=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的拐点,经研究发现,所有的三次函数f(x)=ax3+bx2+cx+d(a≠0)都有拐点,且都有对称中心,其拐点就是对称中心,设f(x)=x3﹣3x2﹣3x+6,则f(![]() )+f(
)+f(![]() )+……+f(
)+……+f(![]() )=_____.
)=_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若存在![]() ,使得
,使得![]() 对任意
对任意![]() 恒成立,则函数
恒成立,则函数![]() 在
在![]() 上有下界,其中
上有下界,其中![]() 为函数
为函数![]() 的一个下界;若存在
的一个下界;若存在![]() ,使得
,使得![]() 对任意
对任意![]() 恒成立,则函数
恒成立,则函数![]() 在
在![]() 上有上界,其中
上有上界,其中![]() 为函数
为函数![]() 的一个上界.如果一个函数既有上界又有下界,那么称该函数有界.下列四个结论:
的一个上界.如果一个函数既有上界又有下界,那么称该函数有界.下列四个结论:
①1不是函数![]() 的一个下界;②函数
的一个下界;②函数![]() 有下界,无上界;
有下界,无上界;
③函数![]() 有上界,无下界;④函数
有上界,无下界;④函数![]() 有界.
有界.
其中所有正确结论的编号为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方形SG1G2G3中,E、F分别是G1G2及G2G3的中点,D是EF的中点,现在沿SE、SF及EF把这个正方形折成一个四面体,使G1、G2、G3三点重合,重合后的点记为G,那么,在四面体S﹣EFG中必有( )
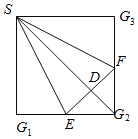
A.SG⊥△EFG所在平面B.SD⊥△EFG所在平面
C.GF⊥△SEF所在平面D.GD⊥△SEF所在平面
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x﹣a|+|x﹣a+1|.
(1)当a=4时,求解不等式f(x)≥8;
(2)已知关于x的不等式f(x)![]() 在R上恒成立,求参数a的取值范围.
在R上恒成立,求参数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() ,
,![]() ,…,
,…,![]() 的项
的项![]() ,其中
,其中![]() …,
…,![]() ,
,![]() ,其前
,其前![]() 项和为
项和为![]() ,记
,记![]() 除以3余数为1的数列
除以3余数为1的数列![]() ,
,![]() ,…,
,…,![]() 的个数构成的数列为
的个数构成的数列为![]() ,
,![]() .
.
(1)求![]() 的值;
的值;
(2)求数列![]() 的通项公式,并化简.
的通项公式,并化简.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com