
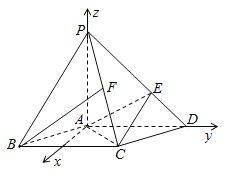
【题目】如图,在底面是菱形的四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() .
.

(1)证明:![]() 平面
平面![]() ;
;
(2)求以![]() 为棱,
为棱,![]() 与
与![]() 为面的二面角的大小
为面的二面角的大小
(3)在棱![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 平面
平面![]() ?证明你的结论.
?证明你的结论.
【答案】(1)证明见解析.(2)![]() .(3)存在;证明见解析.
.(3)存在;证明见解析.
【解析】
(1)根据菱形的性质,结合勾股定理的逆定理、线面垂直的判定定理进行证明即可;
(2)作![]() 交
交![]() 于
于![]() ,根据平行线的性质可以得到
,根据平行线的性质可以得到![]() 平面
平面![]() .
.
作![]() 于
于![]() ,连结
,连结![]() .
.![]() ,
,![]() 即为二面角
即为二面角![]() 的平面角,通过正切的定义求解即可;
的平面角,通过正切的定义求解即可;
(3)以![]() 为原点,
为原点,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,过
轴,过![]() 点且垂直于面
点且垂直于面![]() 的直线为
的直线为![]() 轴,建立空间直角坐标系,可知
轴,建立空间直角坐标系,可知![]() 轴垂直平分
轴垂直平分![]() ,利用空间向量的共线向量的定义,结合线面垂直的判定定理和性质定理进行求解即可.
,利用空间向量的共线向量的定义,结合线面垂直的判定定理和性质定理进行求解即可.
(1)证明:因为底面![]() 是菱形,
是菱形,![]() ,所以
,所以![]() .
.
在![]() 中,由
中,由![]() ,知
,知![]() .同理,
.同理,![]() .所以
.所以![]() 平面
平面![]() ;
;
(2)解:作![]() 交
交![]() 于
于![]() ,由
,由![]() 平面
平面![]() ,知
,知![]() 平面
平面![]() .
.
作![]() 于
于![]() ,连结
,连结![]() .因为
.因为![]() 平面
平面![]() ,所以
,所以![]() ,而
,而![]() ,所以
,所以![]() 平面
平面![]() ,而
,而![]() 平面
平面![]() ,
,
则![]() ,
,![]() 即为二面角
即为二面角![]() 的平面角.
的平面角.
又![]() ,所以
,所以![]() ,
,![]() ,
,![]() .
.
从而![]() ,
,![]() ;
;
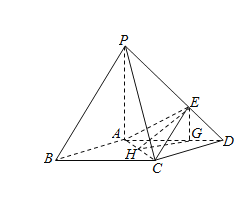
(3)由(1)知![]() 平面
平面![]() ,以
,以![]() 为原点,
为原点,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,过
轴,过![]() 点且垂直于面
点且垂直于面![]() 的直线为
的直线为![]() 轴,建立空间直角坐标系,可知
轴,建立空间直角坐标系,可知![]() 轴垂直平分
轴垂直平分![]() .
.
则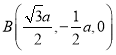 ,
,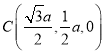 ,
,![]() ,
,![]() .
.
设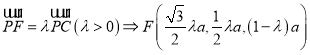 ;
;
∴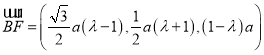 .
.
设![]() 为平面
为平面![]() 的法向量,
的法向量,
则有: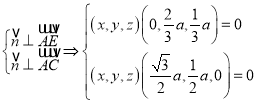
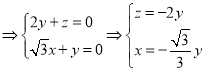 .
.
令![]() 得
得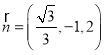 .
.
若![]() 平面
平面![]() ,则有
,则有![]() ,
,
∴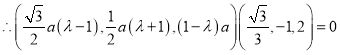 .
.
解得![]() ,此时
,此时![]() 为
为![]() 的中点
的中点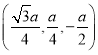 .
.
因此在棱![]() 上存在一点
上存在一点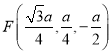 ,使
,使![]() 平面
平面![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,其中左焦点
,其中左焦点![]() (-2,0).
(-2,0).
(1) 求椭圆C的方程;
(2) 若直线y=x+m与椭圆C交于不同的两点A,B,且线段AB的中点M在圆x2+y2=1上,求m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() :
: ![]()
![]() 的离心率为
的离心率为![]() ,上、下顶点分别为
,上、下顶点分别为![]() 、
、![]() ,点
,点![]() 在椭圆上,且异于点
在椭圆上,且异于点![]() 、
、![]() ,直线
,直线![]() 、
、![]() 与直线
与直线![]() :
: ![]() 分别交于点
分别交于点![]() 、
、![]() ,且
,且![]() 面积的最大值为
面积的最大值为![]() .
.
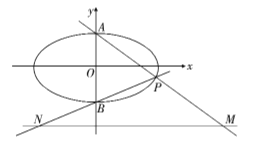
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)求线段![]() 的长的最小值.
的长的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】市场上有一种新型的强力洗衣液,特点是去污速度快.已知每投放![]() (
(![]() ,且
,且![]() )个单位的洗衣液在一定量水的洗衣机中,它在水中释放的浓度
)个单位的洗衣液在一定量水的洗衣机中,它在水中释放的浓度![]() (克/升)随着时间
(克/升)随着时间![]() (分钟)变化的函数关系式近似为
(分钟)变化的函数关系式近似为![]() ,其中
,其中 .若多次投放,则某一时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和.根据经验,当水中洗衣液的浓度不低于
.若多次投放,则某一时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和.根据经验,当水中洗衣液的浓度不低于![]() (克/升)时,它才能起到有效去污的作用.
(克/升)时,它才能起到有效去污的作用.
(1)当一次投放![]() 个单位的洗衣液时,求在
个单位的洗衣液时,求在![]() 分钟时,洗衣液在水中释放的浓度.
分钟时,洗衣液在水中释放的浓度.
(2)在(1)的情况下,即一次投放![]() 个单位的洗衣液,则有效去污时间可达几分钟?
个单位的洗衣液,则有效去污时间可达几分钟?
(3)若第一次投放![]() 个单位的洗衣液,
个单位的洗衣液,![]() 分钟后再投放
分钟后再投放![]() 个单位的洗衣液,请你写出第二次投放之后洗衣液在水中释放的浓度
个单位的洗衣液,请你写出第二次投放之后洗衣液在水中释放的浓度![]() (克/升)与时间
(克/升)与时间![]() (分钟)的函数关系式,求出最低浓度,并判断接下来的四分钟是否能够持续有效去污.
(分钟)的函数关系式,求出最低浓度,并判断接下来的四分钟是否能够持续有效去污.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别为棱
分别为棱![]() ,
,![]() ,
,![]() 的中点.
的中点.

(1)求证:![]()
![]() ;
;
(2)若![]() ,
,![]() ,求三棱锥
,求三棱锥![]() 的体积;
的体积;
(3)判断直线![]() 与平面
与平面![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com