
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,判断并说明函数
时,判断并说明函数![]() 的零点个数.若函数
的零点个数.若函数![]() 所有零点均在区间
所有零点均在区间![]()
![]() 内,求
内,求![]() 的最小值.
的最小值.
【答案】(1)分类讨论,详见解析;(2)![]() 存在两个零点
存在两个零点![]() ,且
,且![]() ,
,![]() ;
;![]() 的最小值为
的最小值为![]() .
.
【解析】
(1)对函数进行求导,根据![]() 的不同取值进行分类讨论,根据导函数的正负性,求出函数的单调性即可;
的不同取值进行分类讨论,根据导函数的正负性,求出函数的单调性即可;
(2)根据![]() ,结合
,结合![]() 的导数
的导数![]() 的性质进行分类讨论求解即可.
的性质进行分类讨论求解即可.
(1)![]() 的定义域为
的定义域为![]()
![]()
当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上单调递增:
上单调递增:
当![]() 时,
时,![]()
所以![]() 在
在![]() 上单调递增:
上单调递增:
当![]() 时,令
时,令![]() ,
,
得![]() ,
,![]() (舍)
(舍)
当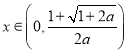 时,
时,![]() ,
,
当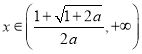 时,
时,![]()
所以![]() 在
在 上单调递增,
上单调递增,
在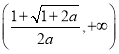 上单调递减.
上单调递减.
综上所述,当![]() 时,
时,![]() 在
在![]() 上单调递增:
上单调递增:
当![]() 时,
时,![]() 在
在 上单调递增,
上单调递增,
在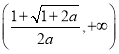 上单调递减.
上单调递减.
(2)当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() 单调递增,
单调递增,
![]() ,
,![]()
则![]() ,故不存在零点:
,故不存在零点:
当![]() 时,
时,![]() ,
,
![]() 在
在![]() 上单调递减,
上单调递减,
所以![]()
所以![]() ,
,![]() 单调递增,
单调递增,
又![]()
![]()
所以存在唯一![]() ,使得
,使得![]()
当![]() 时,
时,![]() ,
,![]() ,
,
所以![]() 单调递减,
单调递减,
![]() ,
,![]()
所以![]() ,存在使得
,存在使得![]()
当![]() 时,
时,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() 单调递减, .
单调递减, .
又![]() ,
,![]()
因此,![]() 在
在![]() 上恒成立,
上恒成立,
故不存在零点.
当![]() 时,
时,![]() ,
,
所以![]() 单调递减,
单调递减,
因为![]() ,
,
所以![]() 单调递减,
单调递减,
又![]() ,
,
所以存在唯一![]() ,使得
,使得![]() .
.
当![]() 时,
时,![]() ,
,
故不存在零点.
综上,![]() 存在两个零点
存在两个零点![]() ,且
,且![]() ,
,![]()
因此![]() 的最小值为
的最小值为![]() .
.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源: 题型:
【题目】为弘扬新时代的中国女排精神.甲、乙两个女排校队举行一场友谊比赛,采用五局三胜制(即某队先赢三局则获胜,比赛随即结束).若两队的竞技水平和比赛状态相当,且每局比赛相互独立,则比赛结束时已经进行的比赛局数的数学期望是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】厂家在产品出厂前,需对产品做检验,第一次检测厂家的每件产品合格的概率为![]() ,如果合格,则可以出厂;如果不合格,则进行技术处理,处理后进行第二次检测.每件产品的合格率为
,如果合格,则可以出厂;如果不合格,则进行技术处理,处理后进行第二次检测.每件产品的合格率为![]() ,如果合格,则可以出厂,不合格则当废品回收.
,如果合格,则可以出厂,不合格则当废品回收.
![]() 求某件产品能出厂的概率;
求某件产品能出厂的概率;
![]() 若该产品的生产成本为
若该产品的生产成本为![]() 元/件,出厂价格为
元/件,出厂价格为![]() 元/件,每次检测费为
元/件,每次检测费为![]() 元/件,技术处理每次
元/件,技术处理每次![]() 元/件,回收获利
元/件,回收获利![]() 元/件.假如每件产品是否合格相互独立,记
元/件.假如每件产品是否合格相互独立,记![]() 为任意一件产品所获得的利润,求随机变量
为任意一件产品所获得的利润,求随机变量![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据某地区气象水文部门长期统计,可知该地区每年夏季有小洪水的概率为0.25,有大洪水的概率为0.05.
(1)从该地区抽取的![]() 年水文资料中发现,恰好3年无洪水事件的概率与恰好4年有洪水事件的概率相等,求
年水文资料中发现,恰好3年无洪水事件的概率与恰好4年有洪水事件的概率相等,求![]() 的值;
的值;
(2)今年夏季该地区某工地有许多大型设备,遇到大洪水时要损失60000元,遇到小洪水时要损失20000元.为保护设备,有以下3种方案:
方案1:修建保护围墙,建设费为3000元,但围墙只能防小洪水.
方案2:修建保护大坝,建设费为7000元,能够防大洪水.
方案3:不采取措施.
试比较哪一种方案好,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点P(x0,y0)在曲线y=x2(x>0)上.已知A(0,-1),![]() ,n∈N*.记直线APn的斜率为kn.
,n∈N*.记直线APn的斜率为kn.
(1)若k1=2,求P1的坐标;
(2)若k1为偶数,求证:kn为偶数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]()
![]() ,如图将
,如图将![]() 分别绕原点
分别绕原点![]() 逆时针旋转
逆时针旋转![]() ,
,![]() ,
,![]() 得到曲线
得到曲线![]() ,
,![]() ,
,![]() .以坐标原点为极点,
.以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.

(1)分别写出曲线![]() 的极坐标方程;
的极坐标方程;
(2)设![]() 交
交![]() 于
于![]() 两点,
两点,![]() 交
交![]() 于
于![]() 两点(其中
两点(其中![]() 均不与原点重合),若四边形
均不与原点重合),若四边形![]() 的面积为
的面积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】桂林漓江主要景点有象鼻山、伏波山、叠彩山、芦笛岩、七星岩、九马画山,小张一家人随机从这6个景点中选取2个进行游玩,则小张一家人不去七星岩和叠彩山的概率为( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农科院为试验冬季昼夜温差对反季节大豆新品种发芽的影响,对温差与发芽率之间的关系进行统计分析研究,记录了6天昼夜温差与实验室中种子发芽数的数据如下:
日期 | 1月1日 | 1月2日 | 1月3日 | 1月4日 | 1月5日 | 1月6日 |
温差 | 10 | 11 | 12 | 13 | 8 | 9 |
发芽数 | 26 | 27 | 30 | 32 | 21 | 24 |
他们确定的方案是先从这6组数据中选出2组,用剩下的4组数据求回归方程,再用选取的两组数据进行检验.
(1)求选取的2组数据恰好是相邻2天数据的概率;
(2)若由线性回归方程得到的估计数据与实际数据的误差不超过1粒,则认为得到的线性回归方程是可靠的.请根据1月2,3,4,5日的数据求出![]() 关于
关于![]() 的线性回归方程(保留两位小数),并检验此方程是否可靠.
的线性回归方程(保留两位小数),并检验此方程是否可靠.
参考公式: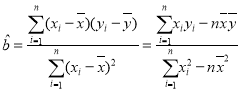 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
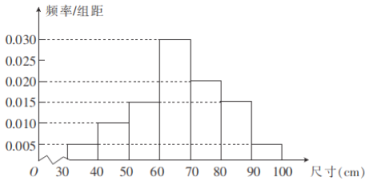
【题目】为了检测生产线上某种零件的质量,从产品中随机抽取100个零件,测量其尺寸,得到如图所示的频率分布直方图.若零件尺寸落在区间![]() 之内,则认为该零件合格,否则认为不合格.其中
之内,则认为该零件合格,否则认为不合格.其中![]() ,
,![]() 分别表示样本的平均值和标准差,计算得
分别表示样本的平均值和标准差,计算得![]() (同一组中的数据用该组区间的中点值作代表).
(同一组中的数据用该组区间的中点值作代表).
(1)已知一个零件的尺寸是![]() ,试判断该零件是否合格;
,试判断该零件是否合格;
(2)利用分层抽样的方法从尺寸在![]() 的样本中抽取6个零件,再从这6个零件中随机抽取2个,求这2个零件中恰有1个尺寸小于
的样本中抽取6个零件,再从这6个零件中随机抽取2个,求这2个零件中恰有1个尺寸小于![]() 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com