练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    （满分12分）某家公司每月生产两种布料A和B，所有原料是三种不同颜色的羊毛，下表给出了生产每匹每种布料所需的羊毛量，以及可供使用的每种颜色的羊毛的总量。
    羊毛颜色
    		每匹需要 / kg
    		供应量/ kg
    布料A
    		布料B
    红
    		4
    		4
    		1400
    绿
    		6
    		3
    		1800
    黄
    		2
    		6
    		1800
    已知生产每匹布料A、B的利润分别为120元、80元。那么如何安排生产才能够产生最大的利润？最大的利润是多少？
    设每月生产布料A、B分别为x匹、y匹，利润为Z元，那么 
         ①          目标函数为
    作出二元一次不等式①所表示的平面区域（阴影部分）即可行域

    把变形为，得到斜率为，在轴上的截距为，随z变化的一族平行直线。如图可以看出，当直线经过可行域上
    M时，截距最大，即z最大。 解方程组
    得M的坐标为x="250" ,  y="100 " 所以  
    答：该公司每月生产布料A、B分别为250 、100匹时，能够产生最大的利润，最大的利润是38000 元。
    略
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：填空题

    实数满足条件，则目标函数的最大值为        .

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

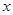    一农民有基本农田2亩，根据往年经验，若种水稻，则每季每亩产量为400公斤；若种花生，则每季每亩产量为100公斤。但水稻成本较高，每季每亩240元，而花生只需80元，且花生每公斤5元，稻米每公斤卖3元。现该农民手头有400元；（1）设该农民种亩水稻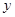，亩花生，利润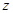元，请写出约束条件及目标函数；（2）问两种作物各种多少，才能获得最大收益？

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    设R且满足，则的最小值等于 (     )
    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本小题满分12分）如果直线与轴正半轴，轴正半轴围成的四边形封闭区域（含边界）中的点，使函数的最大值为8，求的最小值

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    某厂生产甲产品每千克需用原料A和原料B分别为、千克，生产乙产品每千克需用原料A和原料B分别为、千克。甲、乙产品每千克可获利润分别为、元。月初一次性购进本月用原料A、B各、千克。要计划本月生产甲产品和乙产品各多少千克才能使月利润总额达到最大。在这个问题中，设全月生产甲、乙两种产品分别为千克、千克，月利润总额为元，那么，用于求使总利润最大的数学模型中，约束条件为
    A.   B.   C.  D.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    若满足约束条件则的最大值为（     ）
    A．3B．10C．6D．9

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    若实数x，y满足，则的取值范围是          

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    实数的最大值为           ；

    查看答案和解析>>

    同步练习册答案